2021. 12. 15. 03:45ㆍ열 물리학
<Energy of the binary magnetic system>
- elementary magnets are placed in a magnetic field.
- different states, energies are no longer all equal.
the energy of interaction of a single magnetic moment m with a fixed external magnetic field B is

For the model system of “N” elementary magnets, each with two allowed orientations in a uniform magnetic field B, the total potential energy
U is

M is total magnetic moment 2sm
(N is even s= 0,1,2,3...)
the spacing(간격) between adjacent energy level s of this model is constant

[1.10 comment] N=10 magnetic moment m in 자기장 B 2s 는 spin excess, The levels are labeled
by their s

예를 들면

Example: Multiplicity function for harmonic oscillators. The problem of the binary model system is the simplest problem for which an exact solution for the multiplicity function is known.
(오리지널 전개방법은 어려우니 학생들은 걱정 말라고는 하는데 이럴수록 열심히 해보자! 고민 많이 해봤다... 책 해설이 좋진 않아서;;;)
(해설)
조화진동 에너지는

(i) N=1 원자하나 state는 n개

원자가 하나일 땐 그 상태가 될 각 상태의 경우의 수는 각각 하나만 가능하다. (조화진동자)
g(N,n)= g(1,n) = 1
(ii) N=2 원자하나 state는 각각 n개씩

N=2 일 때, g(N,n)=g(2,n) 은 몇 개??-> 축퇴도..!!





이렇다면 g를 수학적으로 나타내기 좋은 방법이 뭐가있을까?
우리가 state를 0,1,2,3,4, ... ,n 으로 표현했었는데,
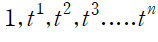
으로 각 state를 표현해보자!

N=1 일때는 각 상태에 원자가 하나만 들어갈 수 있다. g(1,n)=1

사실 state 이름은 중요하지 않다. 어자피 우리는 g만 제대로 표현할 수 있다면 만사 오케이 임!
N=2 일때는

즉 원자 두 개일때는?? 하나가 두개니깐 두 계를 곱한다는 아이디어로 접근해도 되겠죠?

이게 진짜 신기하게 g(2,n) 이 정확히 전개되었다!
N=N 이라면???


g(N,n)을 알기위해 N=1 인 시스템을 N번 곱하여 위와 같은 관계가 만들어졌다.
입자 N 에서

의 경우의 수를 알기 위해 g(N,n)을 위 식에서 뽑아내는 게 목표이다.

(n번 미분해서 남는 term 은 t->0 으로 없애고 , n번 미분하여 내려온 지수들은 n! 만큼 나눠주면 g(N,s) 만 남게된다.)
이 말을 수학으로 표현하면....다음과 같다.
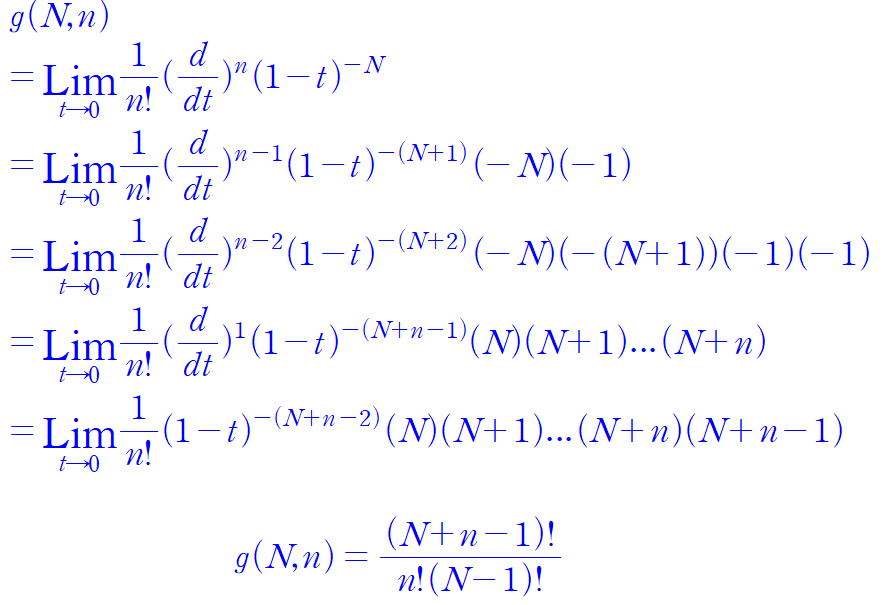
Multiplicity function for harmonic oscillators 를 구할수 있게 되었다.
state 이름을 바꿔주면서 급수의 계산으로 바꿔주는 아이디어가 정말 참신하다. 대부분 책에는 간단하게 나와있으니 이번 글이 도움이 되길 바란다.
'열 물리학' 카테고리의 다른 글
| [열 물리학 11] Probability(확률 ), Ensemble (앙상블) (0) | 2021.12.17 |
|---|---|
| [열 물리학 10] Fundamental assumption of THERMAL PHSYSICS열 물리학에서의 기본가정 (0) | 2021.12.17 |
| [열물리학 08] The binomial distribution (0) | 2021.12.15 |
| [열 물리학 07] Average values (평균값) (0) | 2021.12.15 |
| [열 물리학 06] Sharpness of the Multiplicity Function (0) | 2021.12.15 |