2021. 12. 17. 04:51ㆍ열 물리학
Probability
we have a closed system the we know is equally likely to be in any of the g accessible quantum states.
generalstate label.
The probability P(s) of finding the system in this state is

if the state s is accessible and p(s)=0 otherwise, consistent with the fundamental assumption.
The sum

of Probability over all states is always equal to unity, because the total Probability that the system is in some state is unity:

definition of the average

suppose that the physical property X has the value X(s) when the system is in the state s.
Here X 는 나타낼 수 있습니다. magentic moment, energy, square of the energy, charge density near a point
r (벡터) , or any property that can be observed when the system is in a quantum state
Then the average of the observations of the quantity X taken over a system described by the probabilities P(s) is
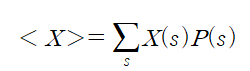
For a closed system, average value of X is

<X>를 ensemble average 라고 부른다.
ex) g개의 similar systems을 생각해보자, one in each accessible(허용된) quantum state. such a group of systems constructed alike is called an ensemble of systems (비슷한 system의 모임을 system ensemble )
집합체의 평균을 ensemble average 이라고 한다.
->The average of any property over the group is called the ensemble average of that property
Ensemble(앙상블)
An ensemble of systems is composed many system, all constructed alike.
->Each system in the ensemble is a replica(복제품) of the actual system in one of the quantum states accessible to the system
(ex 1) For spin system N=10
u=-2smB = -8mB -> 2s =8
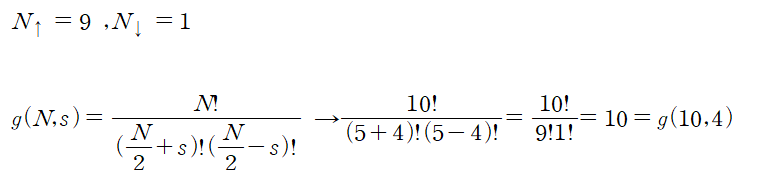


인 상황 a ,b, c, d, ..., j 각 줄들을 ensemble 하나씩이다.
(=replica of the actual system)
(ex2) For N=5 2s =1


(ex3) For N=5, 2s=5
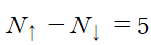

'열 물리학' 카테고리의 다른 글
| [열물리학 13] Thermal equilibrium (열 평형) (0) | 2021.12.22 |
|---|---|
| [열 물리학 12] Most Probable Configuration(최빈 배열) (0) | 2021.12.17 |
| [열 물리학 10] Fundamental assumption of THERMAL PHSYSICS열 물리학에서의 기본가정 (0) | 2021.12.17 |
| [열 물리학 09] Energy of the binary magnetic system (0) | 2021.12.15 |
| [열물리학 08] The binomial distribution (0) | 2021.12.15 |