2021. 12. 17. 06:02ㆍ열 물리학

위와 같이 두 시스템이 있고 입자교환은 없으며 에너지 교환만있는 경우입니다.
Thermal conductor(열 접촉) and insulation (단열)

when 시스템 &_1 +&_2 = & : closed system
Q: 어떻게 에너지를 나누는게 확률이 높을까?
The most probable division of energy = combined system has the maximum number of accessibles
Using the example of two spin systems in a magnetic field
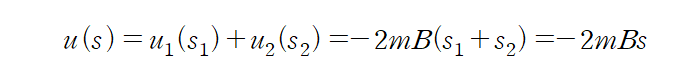

상태 s가 상수가 된다는 사실을 에너지 u로 부터 알게 되었습니다.
그렇다면 두 시스템이 접촉할 때 중복도 함수는 어떻게 될까요?

For g_1g_2 will be a maximum -> most probable configuration
The number of state in the most probable configuration:


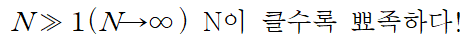
If N is very large (N>>1) sharp maximum is property of real system
-> fluctuations(변동,기울기) about the maximum (most probable configuration becomes very small.)
(앞에서 나왔던.... The most probable division of energy = combined system has the maximum number of accessibles = 그 system의 특징을 만듬.)
average value -> thermal equilibrium
<Example> Two spin system in thermal contact :
잠시 중요한 예제를 한번 보자면 spin 시스템에서의 열 접촉이 일어나면 어떤 상태가 될까??

이전 게시물에서 공부해오던 식이다 기억나길 바란다.
two spin system이 접촉하면

등 다양한 boundary가 생긴다.
각 상태가 접촉하여 생기는 상태수는

이때 우리가 가장 관심있는 지점은 two spin system에서 가장 많이 일어나는 경우인 maximum이 궁금하다. (이때가 거시세계에서 보여지는 특성이기 때문에...)
max 값을 갖는 s 값을
라 하자.


라는 결과가 나온다.
잠시 초등학교 수학으로 넘어가자! 배웠던 기억은 안나는데...

라는 성질이 있다.
<증명>

그렇다면...

(extremum condition 극값조건)
이 성립한다.
최댓값인지 알고싶다면 두 번 미분을 해보면 된다!! 원함수에 log를 취해도 증가감소는 그대로이므로

이계도함수가 음수이므로
-> extremum is maximum
우리가 궁금한 g1g2 의 최대 값에서의 조건을 알고있으니 그 조건을 이용하자!

To investigate(조사하기위해) the sharpness of maximum of g_1g_2
여기서 델타 값은 가장 뾰족한 지점에서 멀어진 지점이라고 보면 됩니다. 우리의 목표는 델타가 얼마나 가면 급격히 값이 감소하는지 판단해보기 위해 해보는 작업으로 봐도 되겠습니다.


얼마나 샤프한가?



에서 최댓값을 갖는

에서 아주 조금 멀어진

에서의 함수 값은

이다.
짜투리 확률
이 부분은 두가지 방향성으로 접근한다. 첫번째는 확률의 상한을 구하여 어림짐작으로 푸는 방법과 정확히 적분계산을 통해서 풀어가는 방법이다. 두가지 방법을 제시하지만 필자 스스로 이해한 만큼 설명해보도록 하겠다.
방법 (1) 확률의 상한을 구하자.


delta 밖에 확률은 어느정도일까?
(comment) 확률의 상한이라고 책에서 명시해놓곤 왜??...라고 생각되게 한다. 상한이 나오는 과정으로는 다음과 같은 생각으로 확장되었다고 본다.

(g_1g_2 의 그래프 형태는 엄청나게 sharp 하니 분모는 대부분 최대 값을 갖는 지점이 dominate 하다.)


여기서
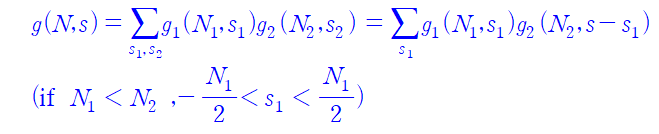
우리가 주목할점은 s_1 의 범위이다. 양의범위가

이니깐 (분자의 개수를 따질 땐 급수는 s_1 에 의존한다는 사실을 잊지말자) 상한값은

를 곱해줘야 한다. (추가로 2는 음의 범위를 고려했기 때문에 양의 범위를 더한 후 2를 곱해야한다.)

대략적으로

정도의 확률의 상한선을 구했다.(힘들었다..)
방법 (2) 정확한 확률계산-적분을 이용한다. (KITTLE PROB 2-6)
calculate approximately the probability that fractional deviation from equilibrium

델타와 입자 N1의 비율이 위와 같다고 주어졌다.

이다.

위 적분표를 이용하여 확률을 조금 더 정확히 구해보자.
----------------------------------------------(풀이)-----------------------------------------
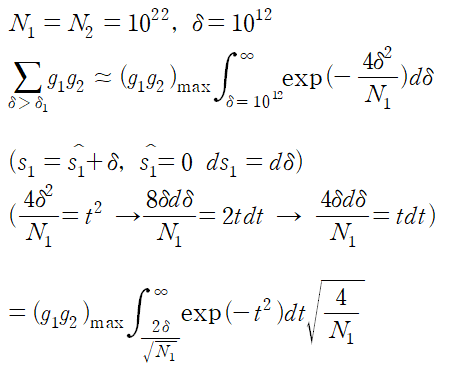

확률이 10^-175 정도라는 건 10^175 번 던져서 로또에 한번 당첨될 확률이라는 이라는 것이다. 우주의 시간보다 오래 걸릴 정도의 수치이다.
'열 물리학' 카테고리의 다른 글
| [열 물리학 14] Law of increase of Entropy (엔트로피 증가법칙) (0) | 2021.12.25 |
|---|---|
| [열물리학 13] Thermal equilibrium (열 평형) (0) | 2021.12.22 |
| [열 물리학 11] Probability(확률 ), Ensemble (앙상블) (0) | 2021.12.17 |
| [열 물리학 10] Fundamental assumption of THERMAL PHSYSICS열 물리학에서의 기본가정 (0) | 2021.12.17 |
| [열 물리학 09] Energy of the binary magnetic system (0) | 2021.12.15 |