2021. 12. 21. 09:32ㆍ전자기학(jackson)
이제부터 난관입니다.
수학은 할만하다 치고 물리학적인 해석이 요구되는 파트입니다.
수식 작성하는데에 시간이 많이드네요


임의의 공간속에서 가지는 potential은 다음과 같다.

-> For volume or surface distributions of charge, the potential is everywhere continuous
그런데 with point or line or dipole layers potential is no longer continuous, as will be seen immediately

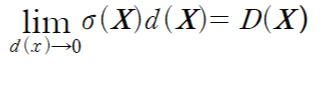
D(X) is dipole -layer distibution of strength distribution on a surface S
임의의 공간에서 dipole 에 의해 생기는 potential 은 다음과 같습니다.



d->0이라면 위와 거의 비슷하겠지만
조금더 미세한변동을 보기위해서 다변수 테일러 전개에 대해서 배워둘 필요가 있습니다.
Taylor series + 다변수

이때

수학자가 좋아하는 것이 쓸데 없는 매개변수하나를 넣어서 지저분하게 만들고 1이나 0을 대입시켜 원래 식으로 바꾸는 방법을 많이 택합니다. (해석학에서 많이 쓰는것 같습니다.)

위 식이 다변수 테일러 전개이다.
(더 길게 전개하려면 파이썬을 이용하자! 일단은 2차 term 까지만 전개하겠다.)
조금 더 풀어서 쓰면 위 식은 다음과 같다.

자 원래의 본론으로 돌아가자면

라는 사실을 알았으니

가 된다는 사실을 알 수 있다.
이때 x가 아닌 a로 미분을 취하고 있다는 것을 인지하자.

다시 본론으로 돌아오면 테일러전개를 배웠으니 이용하면 되겠죠?



이때

라는 것을 잊지말자.
이때 d->0 일때 S 와 S’이 거의 같아 질 것이다. 그리고 da ~ da’ ~da“ 일 것이다.
그러므로

에 의해
면적 변수가 같아지면서 첫번째 항은 없어진다.



왜

가 아닌가? 적분 기호를 포함하지 않은 이유는 그 자체로 아주 작은 dipole 이기 때문이다. 우리는 dipole로 일반적인 potential을 표현하는 것이기 때문에 적분 기호는 dipole 그 자체를 나타내는 것이 아니라 dipole 들의 합을 표현할 뿐이다.
계속해서 적분 기호 안에 식들을 계산해 나가면


잭슨에서 이후 D를 surface-dipole -moment density 라고 한다.
For D is constant

D가 일정하면 모양에 상관없이 potential 이 일정하다.
이 문제를 해결하면서 잊지 말것!
1. observeation point는 영역 S를 기준( S' 이 아니다! )으로 내부에 있다는 것을 명심해야한다. 그렇기 때문에 potential이 음수가 나온다.

2. 우리의 sorce 벡터는 x’ 이다. 그리고 이 sorce의 기준은 dipole 양의 전위를 가지는 disk를 기준으로 d->0 으로 보내지고 있다. 영역 S는 모두 +sigma 의 disk를 기준으로 움직이고 있다는 상황을 생각해야한다.
3. potential 의 차이를 볼 때 역시 +sigma를 기준점으로 시작해 값을 표현해야 한다.
(우리가 이렇게 풀었기 때문에)

바로 위 그림을 통해 점 P에서 전위를 구하면 다음과 같다.

전하가 대칭이니깐 값을 각각 반으로 분배하면 되겠다.
계속해서 +와 – disk 에서의 potential을 각각 생각하면

For d->0

두 dipole 붙은 모습이겠죠??

결과적으로

결론
dipole layer에서 potential 은 불연속이다.
potential drop 은 inside에서 생긴다고한다.
굉장히 작은 영역으로 결과를 얻어냈으니 확장하여 D에 극한을 취하기 전에 값으로 구할 수도 있겠다.
'전자기학(jackson)' 카테고리의 다른 글
| [전자기학 08] green Theorem (그린정리) (0) | 2021.12.31 |
|---|---|
| [전자기학 07] poisson and Laplace Eq (푸아송 그리고 라플라스 방정식) (0) | 2021.12.27 |
| [전자기학 05] scalar potential (0) | 2021.12.21 |
| [전자기학 04] Gauss’s Law 가우스 법칙 (0) | 2021.12.21 |
| [전자기학 03 ] delta function 에 대한 몇가지 성질 (0) | 2021.12.20 |