2021. 12. 31. 06:11ㆍ전자기학(jackson)
전자기학을 공부하기 위해 boundary를 고려해야 하는 것은 필수적이다. 전자기학을 이해하기 위해 많은 수학적 도구를 알아야 한다. 그중 하나인 그린 이론을 공부하고자 한다.
is any Vector function at 부피 V , 표면적 S 의 영역

발산정리에 의해 벡터 A는 다음과 같다.

임의의 벡터이므로 아무 벡터를 넣어도 문제없다.
단 in the volume V bounded by closed surface S 인 벡터를 이용해야 한다.

product Rules

을 이용하고 , A 벡터는 in the volume V bounded by closed surface S 인 아무 벡터이므로

위 두 식을 만들 수 있다.
이때

이 식을 Green’s first identity 이라 한다.
두 식을 빼주면

이다.이 식을 Green’s second identity or Green’s theorem 이라 한다.
각 벡터를 지정해주자.


첫 번째 항만 남기고 나머지는 한쪽으로 몰아주자.

좌변을 x가 V 안에 있을 때, 적분하면 다음과 같다.

결과식 벡터 x 가 V 안에 있을 때

벡터 x가 부피 V의 표면 S를 벗어날 때, 델타함수는 0이 되므로 좌변은 0이 된다.

즉

결론 1
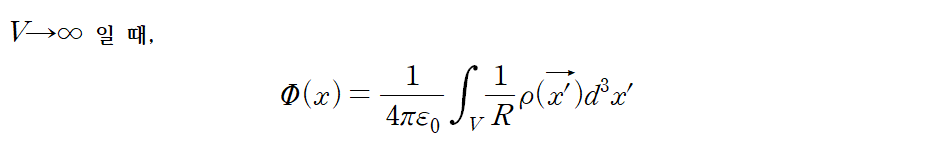
면적적분 term은 1/R 차수만큼 0으로 다가간다.
결론 2
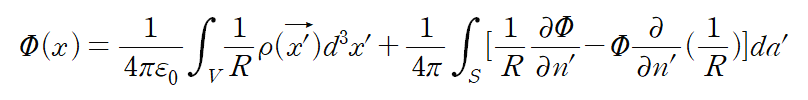
second, for a chargefree volume , the potential anywhere inside the volume is expressed in (1.36) in terms of the potential and its normal derivative only on the surface of the volume.
(둘째, 전하가 없는 체적의 경우 ( ), (식 1.36)에서 부피 내부의 어느 곳에서나 전위는 볼륨의 표면에서의 potential과 그것의 수직 미분으로 표현된다.
(해석 오류가 있다면 수정 덧글남겨주세요!)
이후 potential의 정확한 solution 을 논하기위해 뒤에서 다시 그린정리를 언급할 것입니다.
'전자기학(jackson)' 카테고리의 다른 글
| [전자기학 10] Formal solution of Electrostatic Boundary – value problem with Green function (0) | 2022.01.01 |
|---|---|
| [전자기학 09] uniqueness of the solution with Dirichlet or Neumann Boundary condition (유일성 정리, 경계조건) (0) | 2021.12.31 |
| [전자기학 07] poisson and Laplace Eq (푸아송 그리고 라플라스 방정식) (0) | 2021.12.27 |
| [전자기학 06] surface distributions of charge and Dipole (0) | 2021.12.21 |
| [전자기학 05] scalar potential (0) | 2021.12.21 |