[전자기학 10] Formal solution of Electrostatic Boundary – value problem with Green function

[전자기학 08] 마지막식에서 어리버리 끝났는데( https://zjvlvkdl.tistory.com/40 ), 이번시간에는 전자기학에서의 그린정리의 solution 을 얻어내보자.

 

Greens Function solution to differential Eq with a source function of delta function

 

 

푸아송 방정식은 다음과 같다.

 

 

우리는 1/(거리)의 라플라시안을 취하면 다음과 같은 관계가 됨을 알고 있다.

(아래 식을 부피적분하면 4파이 , x=x’ 일 땐 델타함수가 발산, 그 외일 땐 0 이 된다.)

 

 

 

이때 G를 다음처럼 정의가 된다.

 

 

 

 

이전에 유도했던 1.36 식을 다시 살펴보자.

 

 

잭슨 전자기학 1.36 식

위 식을 그린함수를 이용하여 치환하면 다음과 같다.

 

 

잭슨 전자기학 1.42식

 

 

 

For Dirichlet boundary

Dirichlet boundary는 경계에 대한 식이므로 면적 적분에 있는 G 값만 0이 된다,

부피 적분에서는 0이 아니다.

 

잭슨 전자기학 1.44식

 

 

 

For Neumamn boundary condition

 

neumamn 에서는 더 조심히 다뤄야한다.

G에 경계조건의 명백한(또는 뻔한) 선택은 있는 것처럼 보인다.

 

가 될 것이다.

 

그러나

 

 

잭슨 1.39 식

으로부터

 

 

그리고

 

결과적으로  $G_N$위에서의 가장간단하게 허용되는 neumamn 경계조건은 다음과 같다. (아래식이 될 필요는 없다. 위 적분 조건에 맞기만 하면 아래 식이 달라져도 된다.)

 

 

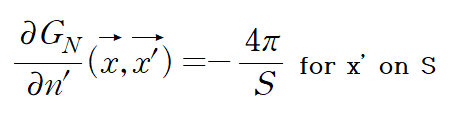
로 둘 수 있다. where S is total area of the boundary surface.

 

 

그때

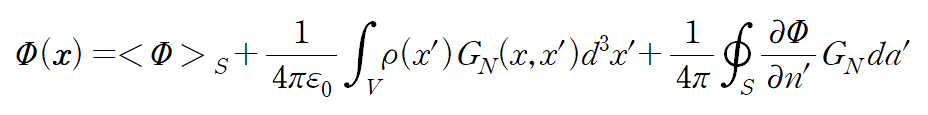
where $<\Phi>_s$ is the average value of the potential over the whole surface.

 

이때 첫번째 항은 다음과같이 유도했다.

 

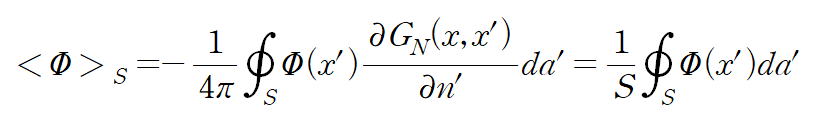
결론

1. if $S   \rightarrow \infty ~~  \Longrightarrow  <\Phi>_s =0$

2. for Dirichlet boundary condition 수학적으로 $G(x,x ')=G(x ',x)$

3. for Neumann boundary condition 는 symmetry is not automatic

4. $F(x,x')/4 \pi  \varepsilon _0$ 의 의미: it is a solution of the Laplace eq inside V and so represents        the potential of a system of charges external to the volume V.