2021. 12. 27. 17:58ㆍ전자기학(jackson)
poisson and Laplace Eq.
이전시간에 보존력을 배웠으니 맥스웰 방정식에 의하여 푸아송 방정식을 유도할 수있다.

이때 값이 0이 되면 라플라스 방정식이라고 한다.

우리는 이전에 스칼라 퍼텐셜을 유도했었다. 그 값은

이것이 푸아송 방정식을 충족시킬까? 그것이 궁금하다.
이전에도 쓰는 방식인 쓸때 없는 term을 만들어서 0으로 보내는 방법으로 1.17식이 푸아송 방정식인지 확인해보는 방향으로 전개하고자한다.

이것을 우리는 그냥 a -potential 이라고 하겠다. 큰의미는 없다.



유도한 분모 term을 대입하면

다변수 테일러전개

위 적분의 0차 term만 들여다보면 4pi가 나온다.

이다.
이것을 증명해보자.

즉 potential 의 0차 term은
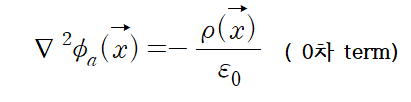
푸아송 방정식을 만족한다.
하지만 의문이 드는데 고차 term은 자연스럽게 무시가 가능할까?? 처음 식으로 돌아오자.
원래 알았어야 할 식은 다음과 같다. 0차 term에 대해서는 알게 되었으니.. other term을 적분을 하면 어떻게 될까?
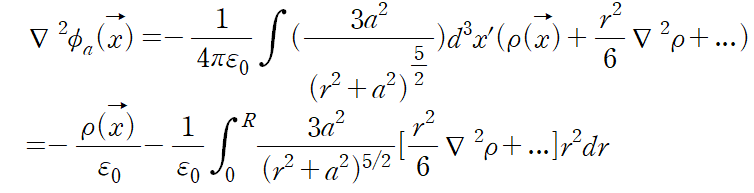
source 의 전개는 다변수 테일러전개를 이용해야하는데.. 왜 이렇게되는지를 모르겠네??
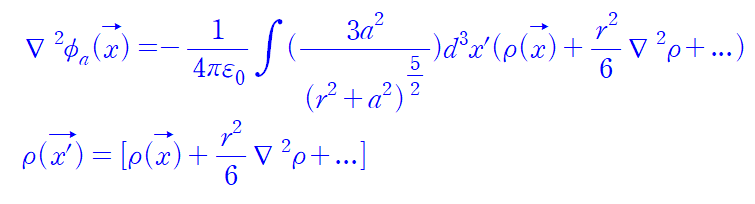
이 식을 유도하기 위해서는 구면좌표계로 치환해줘야 할 필요가 있다. (꽤나 오래 걸린 작업이다.)
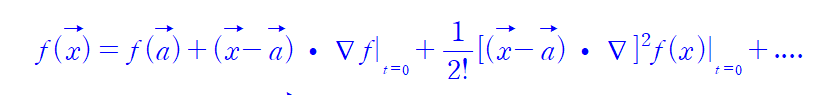
Q: why 1차 term은 사라지며 , 2차 term에 생기는 1/6 은 무엇인가??
1차 term을 보자
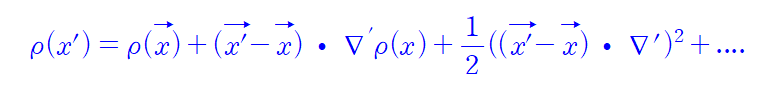
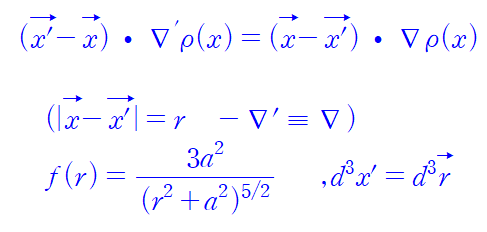

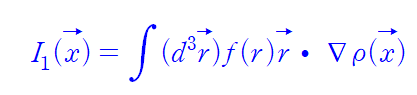
일반성을 잃으면 안되는 것을 또 추가적으로 증명해야 하지만 그렇게 되면 계산이 너무나도 어려워지므로 이때
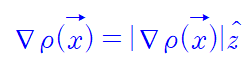
로 선택하고 풀어보자. (훗날 일반화 내용도 추가해보겠다.)
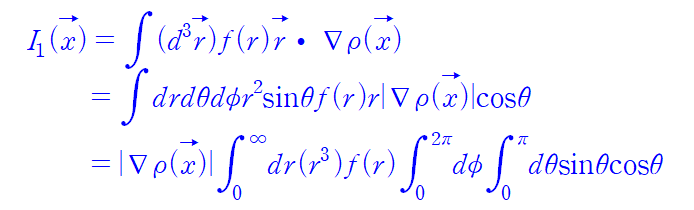
그런데
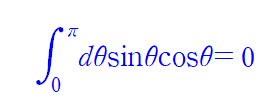
이다.
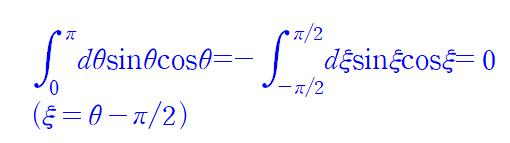
홀수 함수 대칭이므로 0이 됨을 알 수 있다.
2차 term
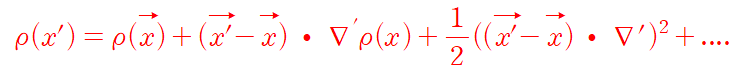
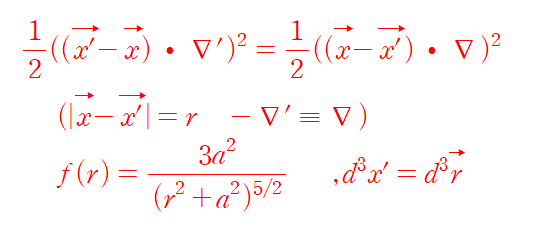
그때
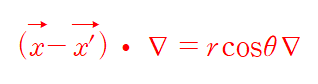
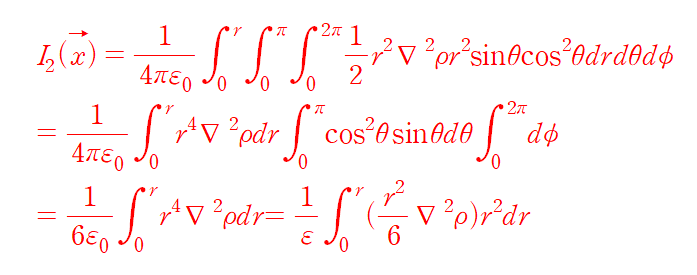
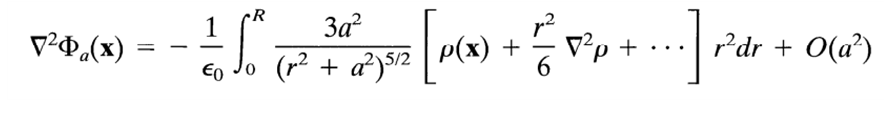
2차 term 역시 잭슨에서 제시한 식과 동일하게 전개되었다.
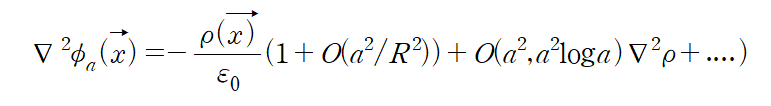
적분 후 식은 위와 같다.
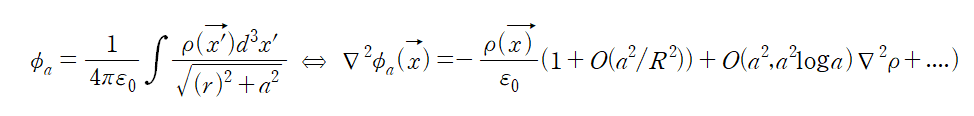
우리가 궁금한 적분의 영역을 생각하면 a->0 으로 가면
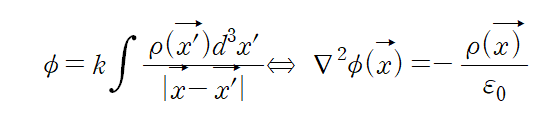
결론적으로 poisson equation 을 얻어낼 수 있다.
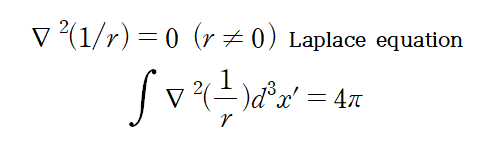
즉
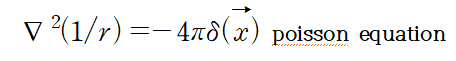
일반화하면
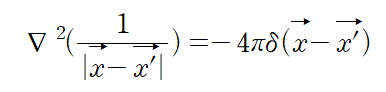
이다.
'전자기학(jackson)' 카테고리의 다른 글
| [전자기학 09] uniqueness of the solution with Dirichlet or Neumann Boundary condition (유일성 정리, 경계조건) (0) | 2021.12.31 |
|---|---|
| [전자기학 08] green Theorem (그린정리) (0) | 2021.12.31 |
| [전자기학 06] surface distributions of charge and Dipole (0) | 2021.12.21 |
| [전자기학 05] scalar potential (0) | 2021.12.21 |
| [전자기학 04] Gauss’s Law 가우스 법칙 (0) | 2021.12.21 |