2022. 1. 2. 07:16ㆍ전자기학(jackson)
이번 포스팅에서는 전기장이 가지는 퍼텐셜 에너지와 에너지 밀도에 대해서 포스팅하고자 합니다.
학부시간에 배웠던 내용보다는 조금 더 일반화된 내용이므로 잭슨 전자기학을 참고해보시면서 보시는것을 추천드립니다.
제가 잭슨 전자기학을 포스팅하는 이유는 잭슨에서 언급하지않고 간단하게 서술한 식을 어떻게 유도했는지에 초점을 맞추고자 합니다. 부족한 내용이 있다면 댓글을 남겨주시면 감사하겠습니다.
전자기학에서 전하가 갖는 일에 정의는 다음과 같다.
work done on the charge is
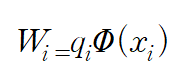

이때 n-1 개의 전하를 띈 입자가 있다고하면 그때의 전위는
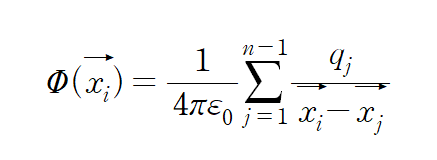
“ j “ is running index
그렇다면 일의 정의에 의해서
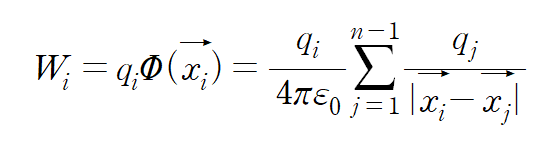
이다.
Total energy

i=j 인 경우를 제외하게 되면서 1/2 factor이 생겼다. 그리고 자기자신을 제외한 갯수를 셌으므로 빠진 만큼 채워내주기위해 마지막항 n-1 ->n 으로 바뀌었다는 것을 인지하자.
For continuons charge distribution(연속 분포에서의 일은?)
마찬가지로 연속이므로 sum 을 극한을 취하면서 적분의 형태로 바뀌었다.

이때 포텐셜의 형태은 다음과 같다.

즉 charge 분포의 총 에너지는
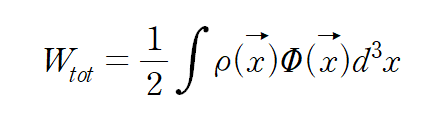
이다.
이때 푸아송 방정식에 의해

이므로

이다.
이때 위 적분을 All space 에 대해서 적분(why? : n is large)을 하자. 부분적분을 적용하면

적분 영역이 all space 이므로

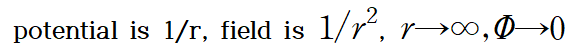
이다.
즉
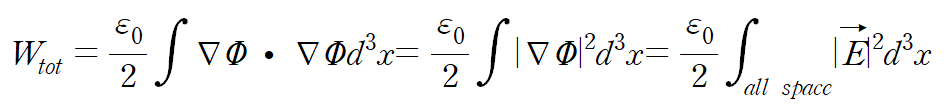
이때
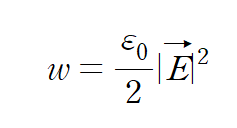
를 Energy density 라고 한다.
여기서 모순이 있다!
energy density를 보니 $w~ \propto |E| ^{2} >0$ 즉 양수이다.
하지만 +q 전하와 –q를 만났을 땐 생기는 에너지는 $W=-k \frac{{q ^{2}}}{{r} } <0$ 음수이다.
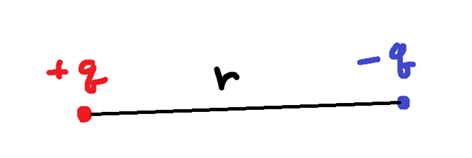
무엇이 틀렸는가???
$|E|^2 $은 자기 자신 에너지 (self energy)
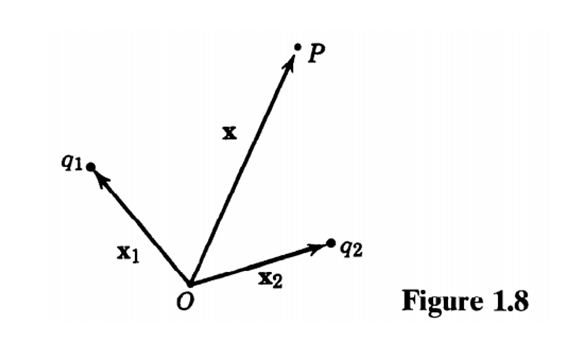
가정: q1,q2 전하가 x1,x2에 있고, P 위치에서 작용하는 전기장은 다음과 같다.
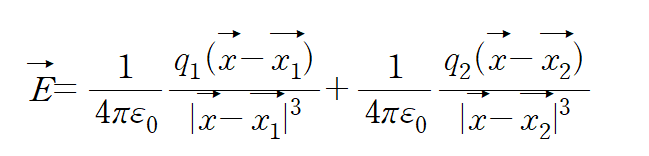
이때 energy density는
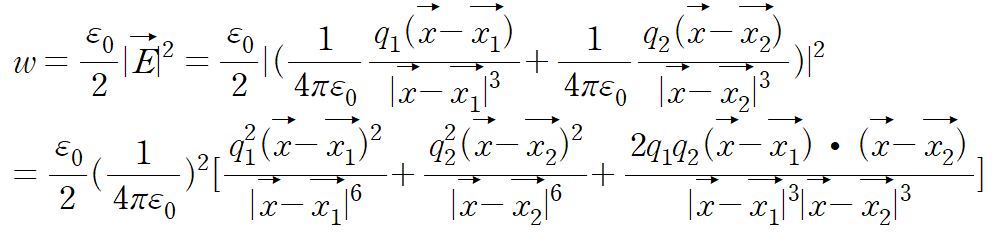
첫 번째 두 번째항은 “self- energy” 라고 한다. 그리고 나머지 세 번째항을 “ interaction potential energy“ 이라고 한다.
모순의 이유: “self- energy” 아까 전개했던 아래의 sum 식에서는 self energy 를 포함시키지 않았다.
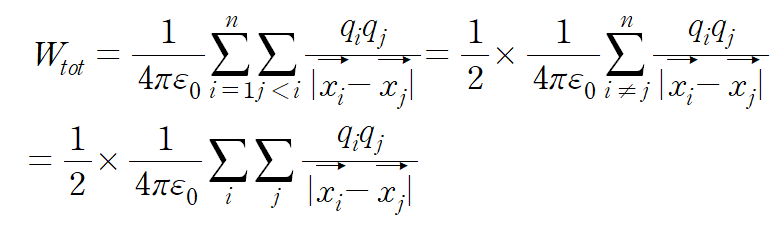
하지만 summation을 아래 적분으로 바꾸는 과정에서 i=j term이 포함되있다.
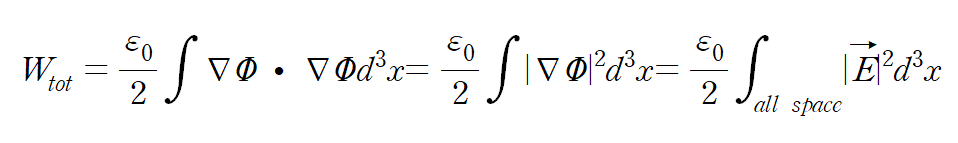
위 에너지 밀도 식(잭슨 1.56식, 식밑에 식 번호를 봐주길 바란다. ) “self- energy” 의 첫 번째 term만 확인해보면
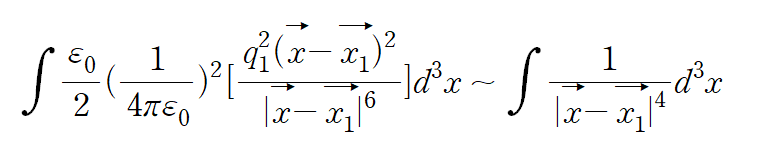
이다. 이때 $\vec{x} \longrightarrow \vec{x_1} $ 일 때, 위 적분은 발산한다. (single charge is self energy)
이제 나머지 interaction energy density인 세 번째 항만 들여다보자.
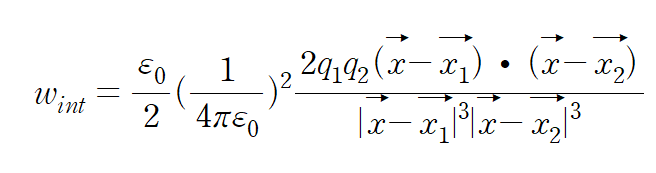
이때, interaction energy 는
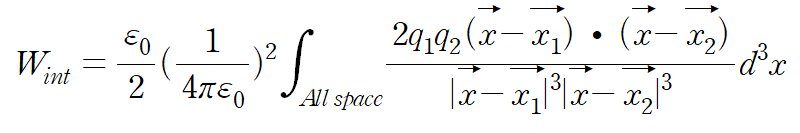
이다. 적분을 하기위해 변수를 치환하자.
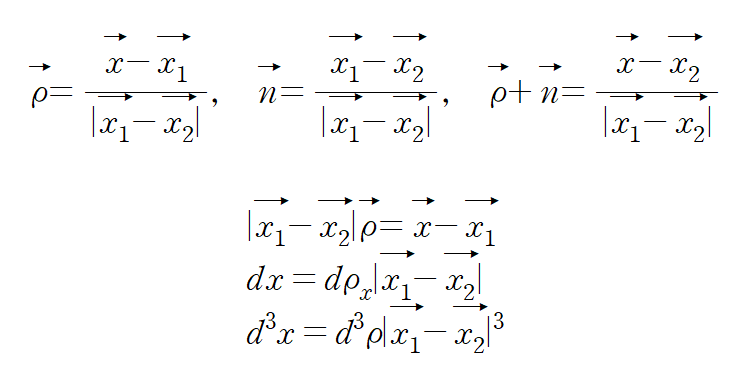
다시 위 적분을 들여다보면
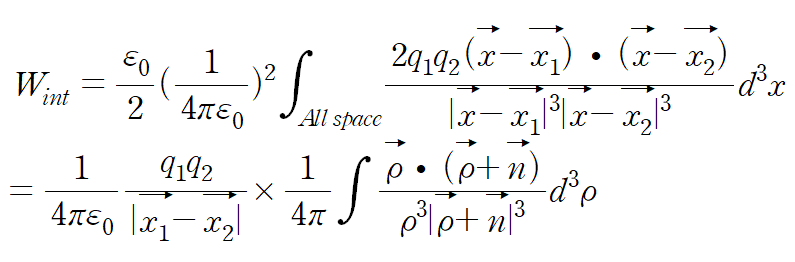
이다.
잭슨 아저씨는
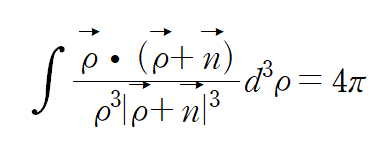
라고 주장하고 있다.(정말?)
---------------------------------------------------------------------------------------------------------------------------------
prove
우리는 다음 식
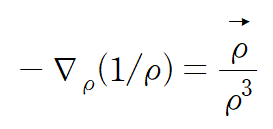
임을 주장할 수 있다.
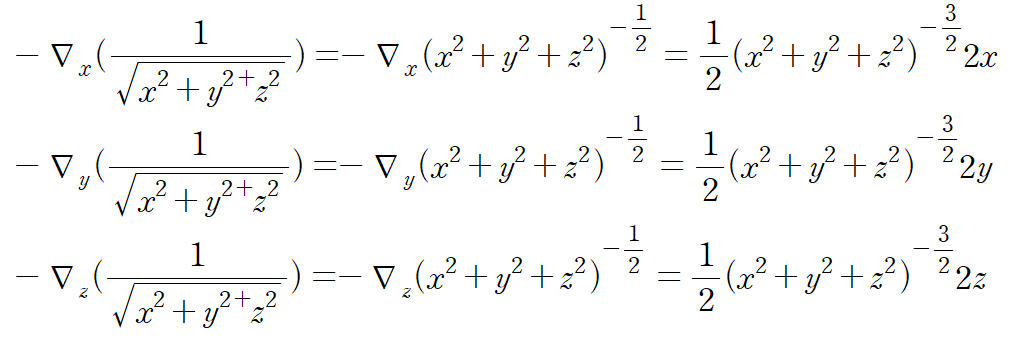
즉
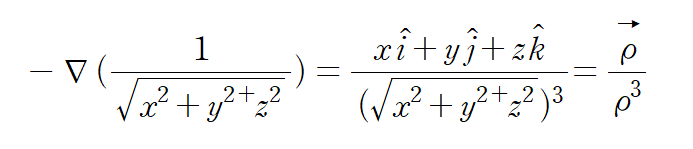
비슷하게
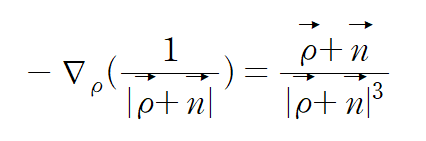
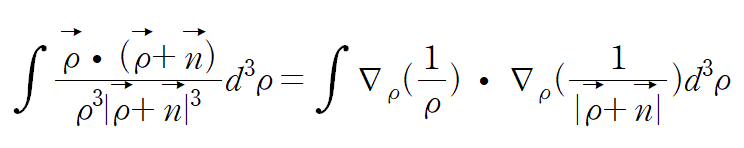
임을 알 수 있다.
곱셈 법칙에 의해
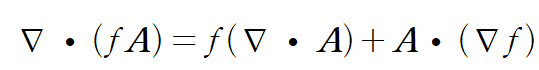
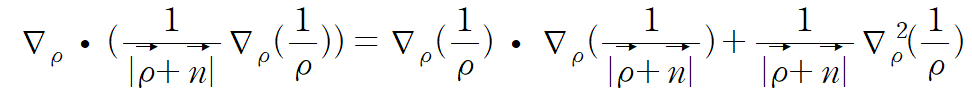
즉
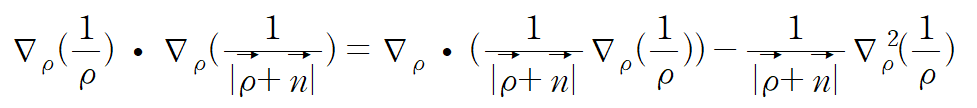
이므로
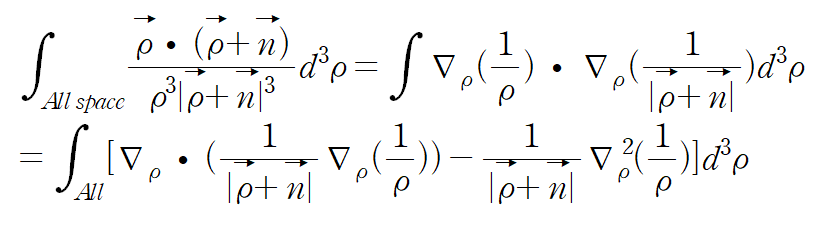
적분 구간이 전 구간($\rho \rightarrow \infty $)이므로 첫 번째 항은 0으로 다가간다.
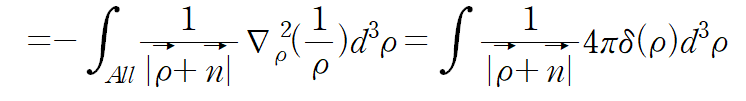
델타함수의 성질의 의해
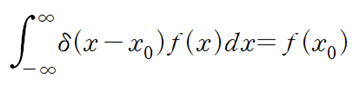
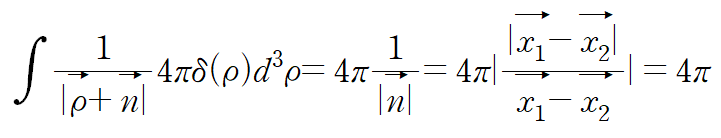
------------------------------------------------------------------------------------------------------------------------------
결과적으로 interaction energy 는 다음과 같다.

$q _{1} q _{2} <0$ 이면, $W _{"int"} <0$ 가 가능해진다. (모순이 없어짐)
------------------------------------------------------------------------------------------------------------------
[Example] on surface of a conductor with a surface charge density $\sigma ( \vec{x}) $
이때 면 전하로부터 나오는 energy density는
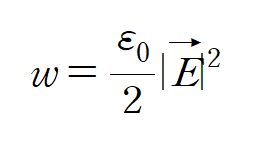
여기서 걸리는 도체에 전기장 E는 무엇일까?
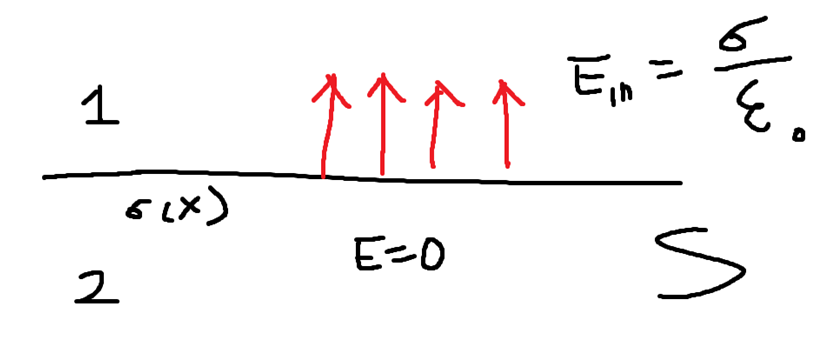
도체의 경계조건을 고려하면 다음과 같습니다.
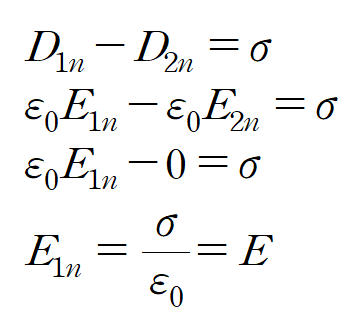
즉 도체 밖에서의 energy density 는
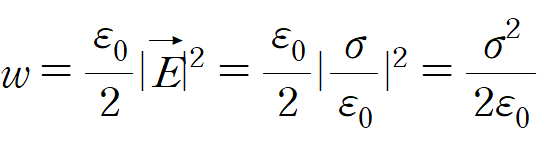
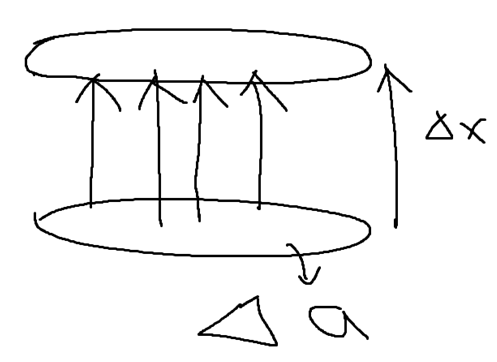
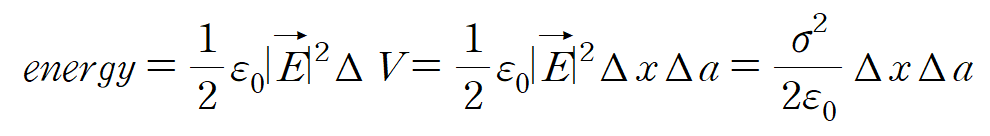
이때 $\Delta x$는 밖으로 면 전하에서 밖으로 뻗어나가는 방향의 변위이다.
하지만 전기장 내에서 전하가 하는 일을 보려면 변위가 $- \Delta x$방향으로 전기장과 같은 힘을 주어야 한다.
그때 면 전하로 인한 전기장으로부터 $ \Delta V$ 내에서 전하가하는 일은
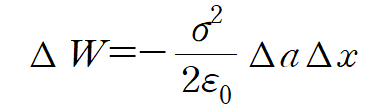
이다.
그때의 힘은
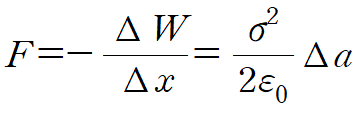
그때의 압력은
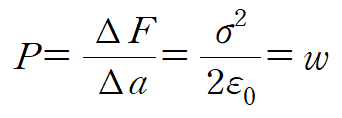
-----------------------------------------------------------------------------------------------------------------
축전기 conductor
간단하게 축전기에 언급하겠다.
For a system of n conductor of surface, each with potential $V_i$ and total charge $Q_i$(i=1,2,3...,n) in otherwise empty space.(표면의 n 도체 시스템의 경우, 각각 전위 Vi와 총 전하 Qi (i=1,2,3...,n) 가 다른 빈 공간에 있습니다.)
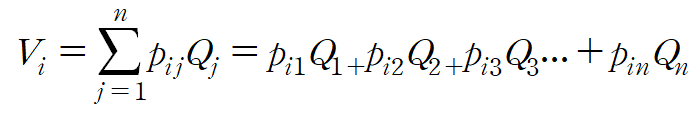
$p_{ij}$ 는 축전기의 기하학적인 계수이다.
그리고 축전기가 가지는 전하량은 다음과 같다.
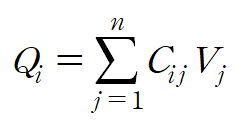
the coefficients $C_{ii} $ are called capacities or capacitances
while(하지만) the $C_{ij},(i \neq j) $ 이면 coefficients of induction (유도 계수) 이라고 한다.
$p_{ij}$ 와 $C_{ij}$는 텐서라는 정도만 알고 넘어가 보자.
'전자기학(jackson)' 카테고리의 다른 글
| [전자기학] 잭슨의 광기 (2.25 식 증명) (0) | 2022.07.11 |
|---|---|
| [전자기학 10] Formal solution of Electrostatic Boundary – value problem with Green function (0) | 2022.01.01 |
| [전자기학 09] uniqueness of the solution with Dirichlet or Neumann Boundary condition (유일성 정리, 경계조건) (0) | 2021.12.31 |
| [전자기학 08] green Theorem (그린정리) (0) | 2021.12.31 |
| [전자기학 07] poisson and Laplace Eq (푸아송 그리고 라플라스 방정식) (0) | 2021.12.27 |