2022. 1. 1. 08:53ㆍ전자기학(jackson)
[전자기학 08] 마지막식에서 어리버리 끝났는데( https://zjvlvkdl.tistory.com/40 ), 이번시간에는 전자기학에서의 그린정리의 solution 을 얻어내보자.
Greens Function solution to differential Eq with a source function of delta function
푸아송 방정식은 다음과 같다.

우리는 1/(거리)의 라플라시안을 취하면 다음과 같은 관계가 됨을 알고 있다.
(아래 식을 부피적분하면 4파이 , x=x’ 일 땐 델타함수가 발산, 그 외일 땐 0 이 된다.)

이때 G를 다음처럼 정의가 된다.

이전에 유도했던 1.36 식을 다시 살펴보자.

위 식을 그린함수를 이용하여 치환하면 다음과 같다.

For Dirichlet boundary

Dirichlet boundary는 경계에 대한 식이므로 면적 적분에 있는 G 값만 0이 된다,
부피 적분에서는 0이 아니다.

For Neumamn boundary condition
neumamn 에서는 더 조심히 다뤄야한다.

G에 경계조건의 명백한(또는 뻔한) 선택은 있는 것처럼 보인다.

가 될 것이다.
그러나
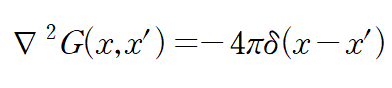
으로부터
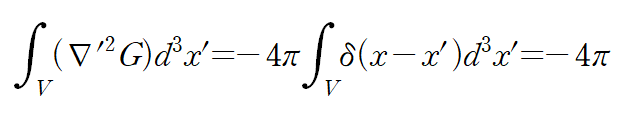
그리고


결과적으로 $G_N$위에서의 가장간단하게 허용되는 neumamn 경계조건은 다음과 같다. (아래식이 될 필요는 없다. 위 적분 조건에 맞기만 하면 아래 식이 달라져도 된다.)
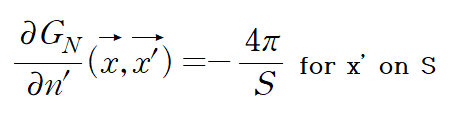
로 둘 수 있다. where S is total area of the boundary surface.
그때
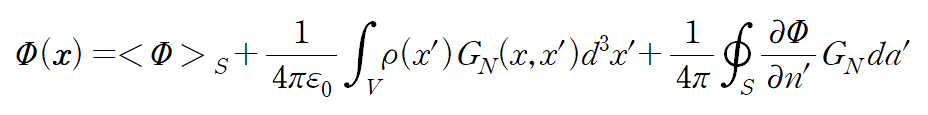
where $<\Phi>_s$ is the average value of the potential over the whole surface.
이때 첫번째 항은 다음과같이 유도했다.
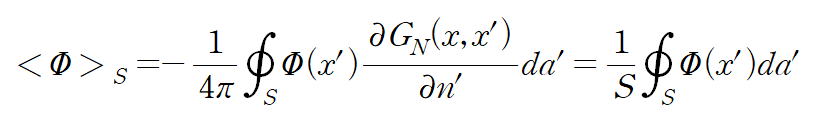
결론
1. if $S \rightarrow \infty ~~ \Longrightarrow <\Phi>_s =0$
2. for Dirichlet boundary condition 수학적으로 $G(x,x ')=G(x ',x)$
3. for Neumann boundary condition 는 symmetry is not automatic
4. $F(x,x')/4 \pi \varepsilon _0$ 의 의미: it is a solution of the Laplace eq inside V and so represents the potential of a system of charges external to the volume V.
'전자기학(jackson)' 카테고리의 다른 글
| [전자기학] 잭슨의 광기 (2.25 식 증명) (0) | 2022.07.11 |
|---|---|
| [전자기학 11] Electrostatic potential Energy and energy Density; capacitance (정전기 전위 퍼텐셜 에너지 그리고 에너지 밀도 ; 전기용량 ) (0) | 2022.01.02 |
| [전자기학 09] uniqueness of the solution with Dirichlet or Neumann Boundary condition (유일성 정리, 경계조건) (0) | 2021.12.31 |
| [전자기학 08] green Theorem (그린정리) (0) | 2021.12.31 |
| [전자기학 07] poisson and Laplace Eq (푸아송 그리고 라플라스 방정식) (0) | 2021.12.27 |