2021. 12. 27. 00:43ㆍ열 물리학
Thermaodynimic proerties as a function of temperation.
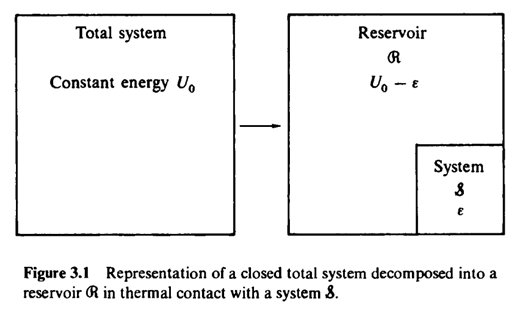
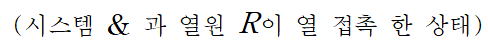



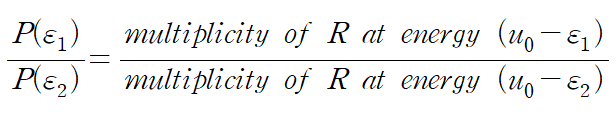
[comment] 열역학의 기본원리에 의해 열원과 시스템은 closed system 이므로 선험적 동등확률[principle of equal a priority probability]을 적용할 수 있다. (고립계는 허용된 양자상태중 어떤 상태에라도 동등하게 머물 수 있다는 것이 열역학의 기본 가정이다.이때 허용된 양자상태는 동등한 확률을 갖는다고 가정한다.)
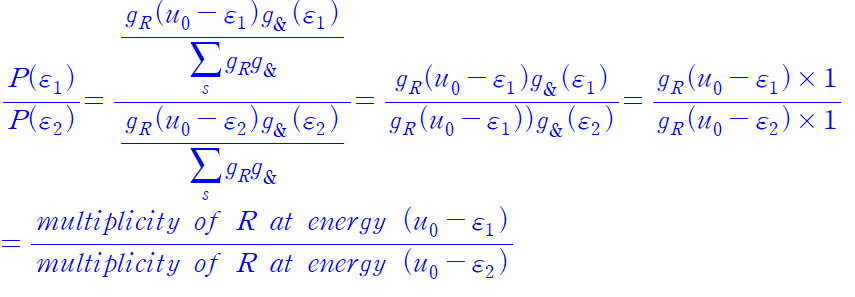
선험적 동등확률을 적용한 결과이다.
If the reservoirs are large
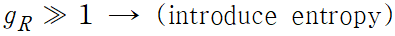

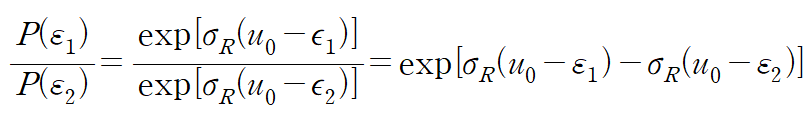
with
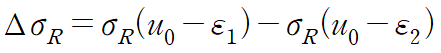
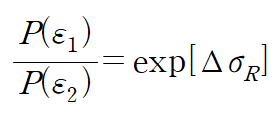

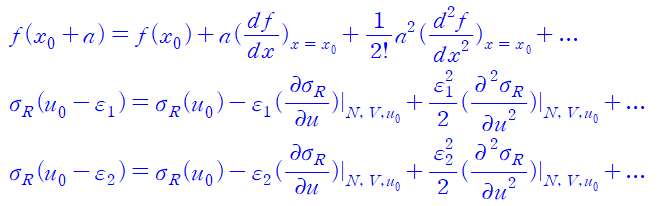
테일러전개를 잊지 않길 바란다.
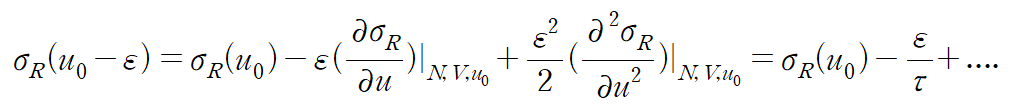
where
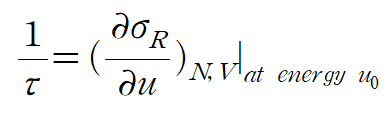
higher order terms vanish in the limit of infinitely large reservoir
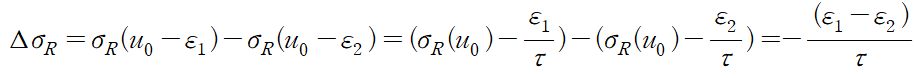
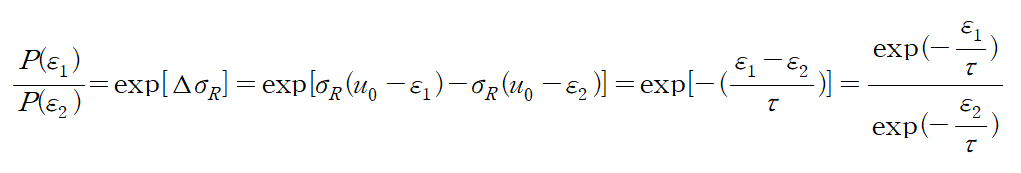

Partition function (분배함수):
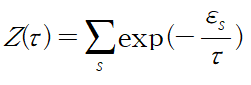
where summation is over Boltzmann factors
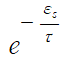
for all states s of the system
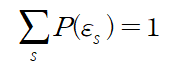
[summation over all probabilites is unity]
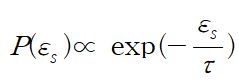
이라는 것을 알았으니.. 임의의 상수를 곱해서 등호로 바꿔야 한다. 근데 하필 확률이니깐 모든 상태의 합을 분모로 보내면 정확한 확률이 될 것이다. 이럴 때 쓰라고 나온 분배함수!
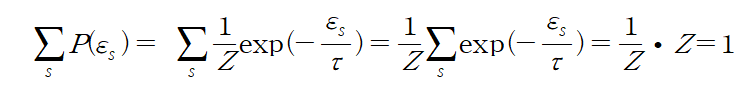
*열 평균에너지에서 Thermal average energy

< > :thermal average (ensemble average): average energy refers to those states of a system that can exchange energy with a reservoir(평균 에너지는 저장소와 에너지를 교환할 수 있는 시스템의 상태를 말합니다.)
[Example: Energy and heat capacity of a two – state system] We treat a system of one particle with two states, one of energy 0 and one of energy $ \varepsilon $. The particle is in thermal contact with a reservoir at temperature $\tau $. We want to find the energy and the heat capacity of the system as a function of the temperature $\tau $. The partition function for the two states of the particle is
[two states E=0, E= $ \varepsilon $]
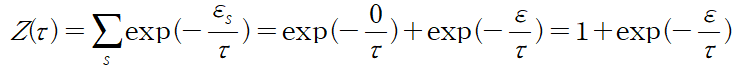
(i) 직접 구하기
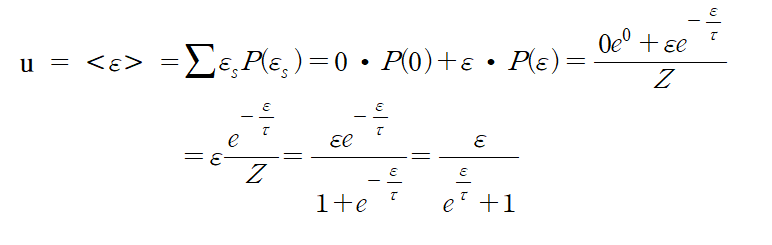
(ii) 수학적 공식
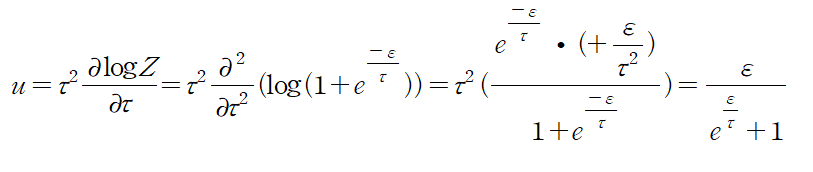
The average energy
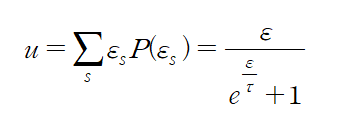
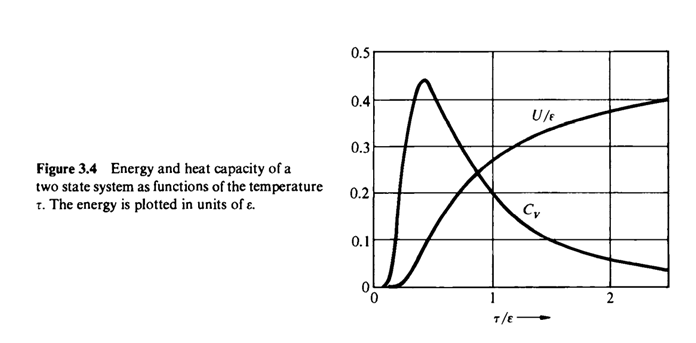
Heat capacity at constant Volume $C_v $ [정적 열용량]

이 식은 뒤에서 다시 전개할 것이다.
(note)
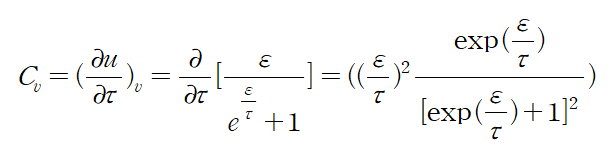
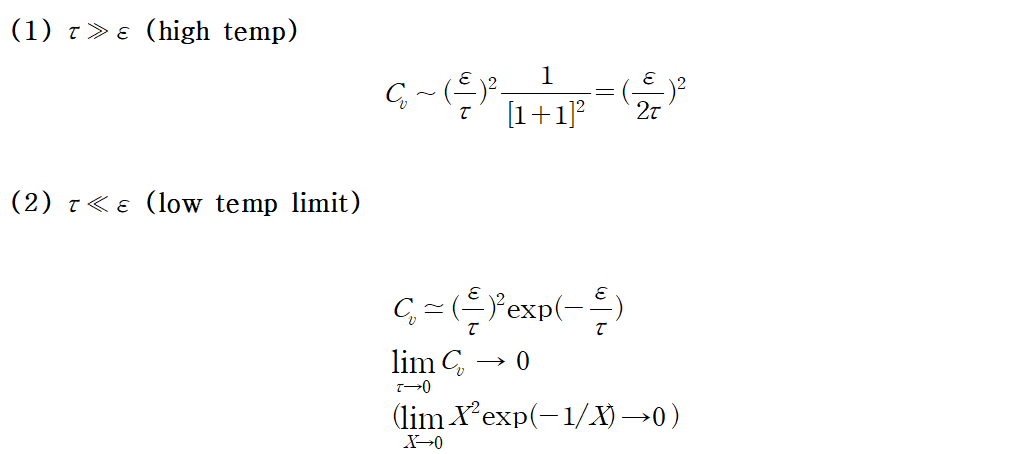

$C_v$ : hump(언덕) is called as a schotty anomaly
'열 물리학' 카테고리의 다른 글
| [열 물리학 20] Thermodynamic Identity (열역학 항등식) (0) | 2021.12.30 |
|---|---|
| [열 물리학 19] reversible process (가역과정) 그리고 Pressure (압력) (0) | 2021.12.30 |
| [열 물리학 17] Perpetual Motion ( 영구 운동) (0) | 2021.12.27 |
| [열 물리학 16] Entropy as a Logrithm (0) | 2021.12.26 |
| [열 물리학 15] Law of Thermodynamics 열역학 법칙 (0) | 2021.12.25 |