2021. 12. 30. 02:59ㆍ열 물리학
정의 : reversible process (가역과정)
A process is reversible if carried out in such a way that the system is always infinitesimally close to the equilibrium condition.
if the entropy is a function of the volume, any change of volume must be carried out so slowly that the entropy at any volume V is closely equal to the equilibrium entropy $\sigma (V)$
-> the entropy is well defined at every stage of a reversible process, and by reversing the direction of the change the system will be returned to its initial condition.
In reversible processes, the condition of the system is well defined at all times
isentropic reversible process(등 엔트로피) (발음이 이스엔트로픽)
A volume change that leaves the system in the same quantum state
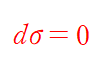
비가역이 뭔가? 풍선 -> 펑 -> Now 하지만 반대과정은 불가능하다.
<Pressure > 압력
consider a system in the quantum state s of energy $\varepsilon _s (V)$
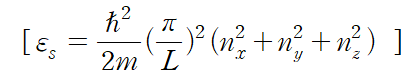
에너지는 체적의 함수이다.
volume is decreased slowly from $V $ to $V - \Delta V$ by an external force.
[The volume change takes place sufficiently slowly that the system remains in the same quantum state $s$ ]
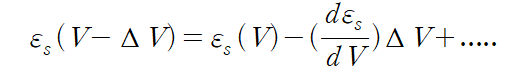
$ \varepsilon _s(V - \Delta V) $ :energy of states after the reversible Volume change
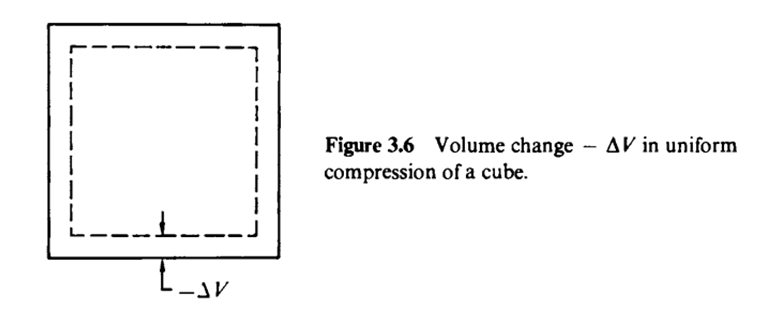
Volume charge $ \Delta V $ by uniform compression(압축) of cube
consider a pressure $ p_s $ applied normal to all face of cube
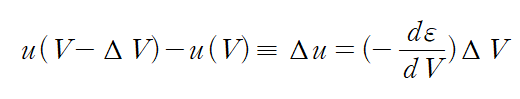
A : area of the cube (큐브 면적)
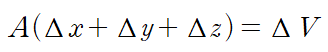
if all the increment
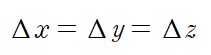
and taken to be positive in the compression (압축).
$\Delta u$=(the work done in the compression) = $ P_s \bullet \Delta V = P_s \bullet A(\Delta x+\Delta y +\Delta z )$
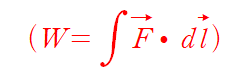
now
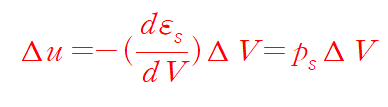
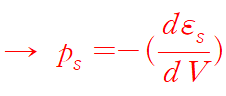
[pressure on a system in the state s]
If we average above eq over all quantum states s, thermal average pressure
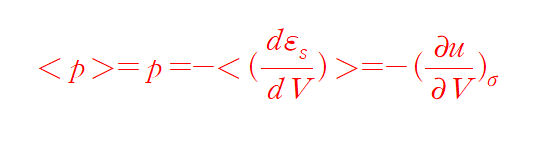
(상태 s를 유지해오면서 전개했기 때문에 $ sigma $ 는 일정하다. (가역조건))
★ other expessions for pressure
$ \sigma = \sigma( u,V) $ for a fixed number of particles
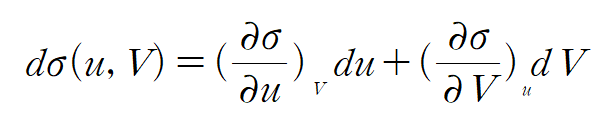
[differential change of entropy for arbitrary independent differential change du & dV ]
If we select du and dV independently in such a way that two terms on the right hand side cancel
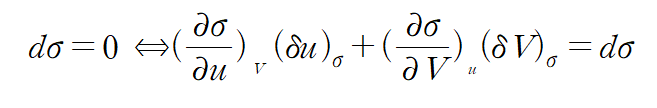
$ (\delta V)_ \sigma $로 나누자 이때 $ \delta $ 는 변수의 막연한 변화 값이다. 엔트로피는 고정되있다.
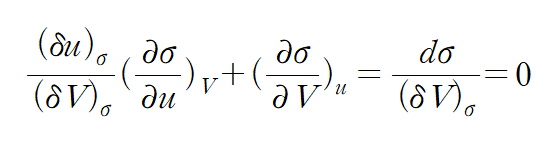
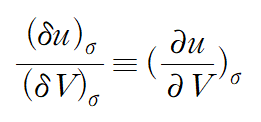
각 변수가 엔트로피가 고정된 상황에서의 변화량의 비율이니 이것은 편미분으로 보아도 되겠다.
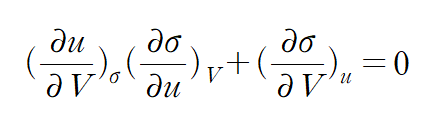
앞에서 공부했듯 엔트로피를 에너지로 미분하면??? 1/(온도) 인 것을 배운 적이 있습니다.
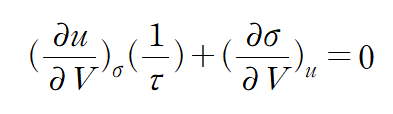
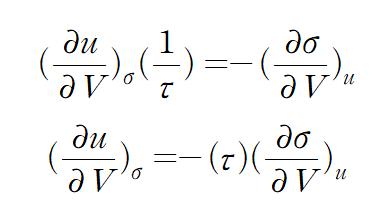
여기서 잠시 차원을 생각해보자.
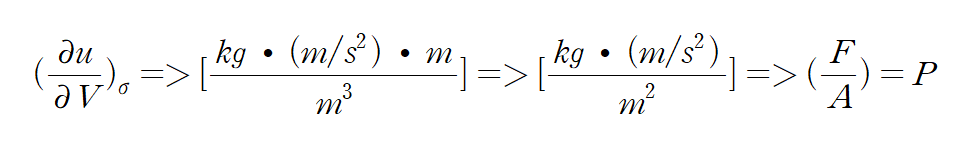
이 식은 압력이라는 사실을 알 수 있다. 이미 앞에서 이 얘기를 위해서 배우긴 했다.
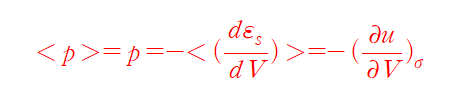
결과적으로
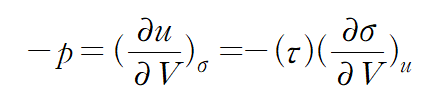
압력에 관한 식 두 개를 알게 되었다!
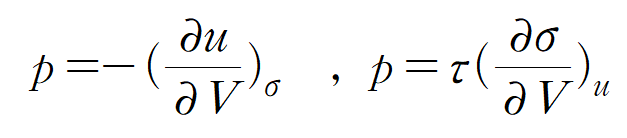
'열 물리학' 카테고리의 다른 글
| [열 물리학 21] Helmholtz free energy (헬름홀츠 자유에너지) (0) | 2021.12.30 |
|---|---|
| [열 물리학 20] Thermodynamic Identity (열역학 항등식) (0) | 2021.12.30 |
| [열 물리학 18] Boltzman distribution function (볼츠만 분포함수) (0) | 2021.12.27 |
| [열 물리학 17] Perpetual Motion ( 영구 운동) (0) | 2021.12.27 |
| [열 물리학 16] Entropy as a Logrithm (0) | 2021.12.26 |