2021. 12. 30. 03:58ㆍ열 물리학
free energy는 고전역학에서도 볼 수 없었던 새로운 변수이다.
열 통계물리를 공부하면서 free energy를 정의해보고 무엇인지 알아보자.
앞에서 공부한 열역학 항등식은 다음과 같다.

이때

라는 값을 정의하고 이것을 Helmholtz free energy 라고 하겠다.
F: important at the constant temperature
(note) How to balance the conflicting(모순) demands of a system for minimum energy and maximum entropy
(note) F will be a minimum for a system on thermal contact with a reservoir if the volume is constant.
(proof) F is an extremum at constant
τ and constant V
F infinitesimal reversible transfer from resorvoir R to system s.

but 앞서 가정에서 부피가 일정 하니깐

(note: the above extremum is minimum)


now σR(u) is constant

in (평형) is 엔트로피 maximum with respect us
결론
σ -> F min with respect us at the most probable configuration
(note) The free energy of the system at constant temperature and constant volume will increase for any departure from the equilibrium configuration.
->평형에서부터 벗어나면 F 값이 커진다.
->F가 가장 작을 때 평형이다.
-----------------------------------------------------------------------------------------------------------------------------------
Example: minimum property of the free energy of a paramagentic (상자성체) system
N 스핀에 관한 g는 이미 예전 포스팅에서 공부했다. 스털링근사로 전개해왔던 식들인데 그중 하나가 다음과 같았다.
(kitel-Thermal physics 1.31식)

이 식을 조금 정리하면
total particle

spin excess

그리고 N is large 이면, 위 식의 첫 번째 항은 무시된다.
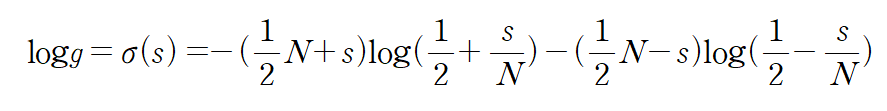
free energy라는 것을 배워봤으니 이용해보자.
그중 다음과 같이
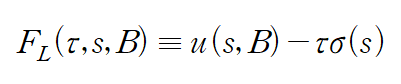
자기장, 상태, 온도를 변수를 갖는 형태인 landau 함수라고 한다.
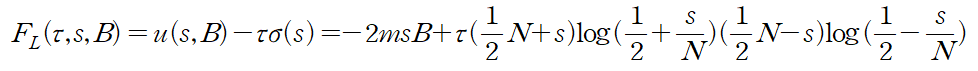
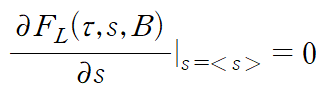
극값에서 최대 최소가 발생하기 때문에 미분해서 0이 되는 것이 우리의 목표이다.
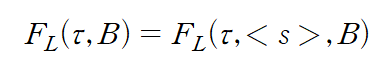
<s> is a function of τ and B
for FL is at the minimum, equilibrium free energy
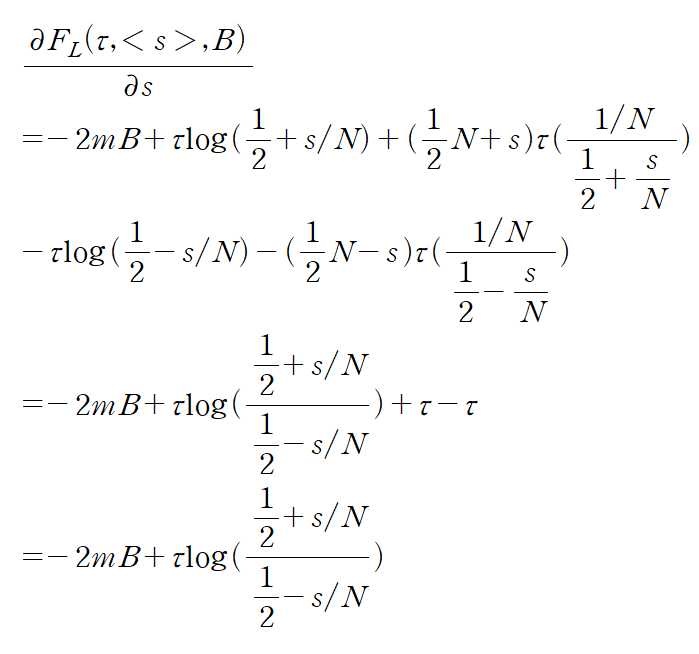
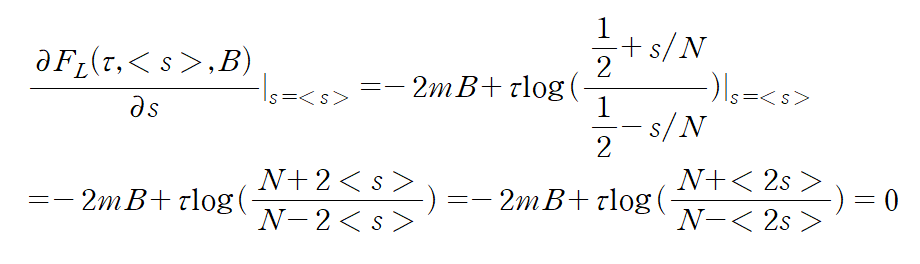
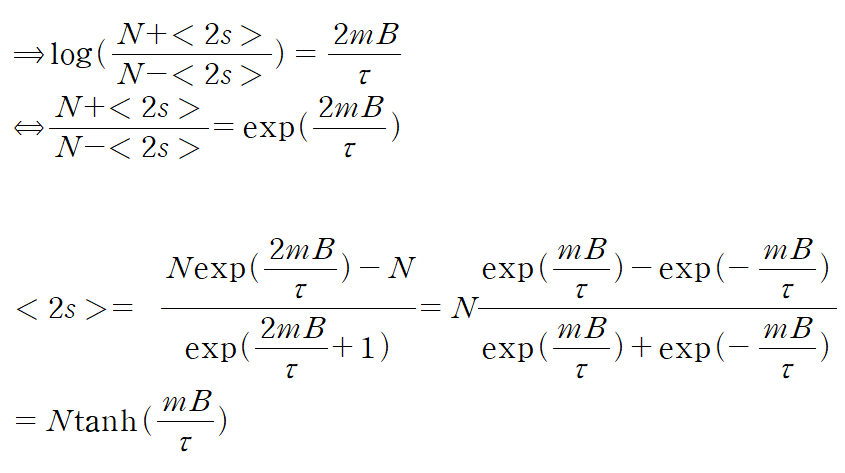
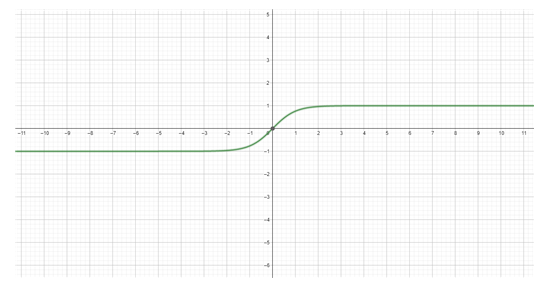
F가 최소를 가질 때(엔트로피가 가장 클 때) spin excess <2s>는 하이퍼볼릭 탄젠트함수의 형태이다. <2s> 함수가 갖는 변수는 입자수, 질량, 자기장, 온도이다.
[comment] free energy 의 평형점인 s=<s> 임을 주목하자 spin system에서 가장 엔트로피가 큰 지점은 함수의 평균지점이었다. 그렇기 때문에 <s>의 평균이 평형점을 갖는 s이다.
이렇게 <2s>를 구했지만 반대로 생각하면 입자 수, 질량, 자기장, 온도만 알고 있으면 <2s>를 알고 s= <2s> 에서의 중복도를 알 수 있고 엔트로피 free energy 까지 알 수 있다.
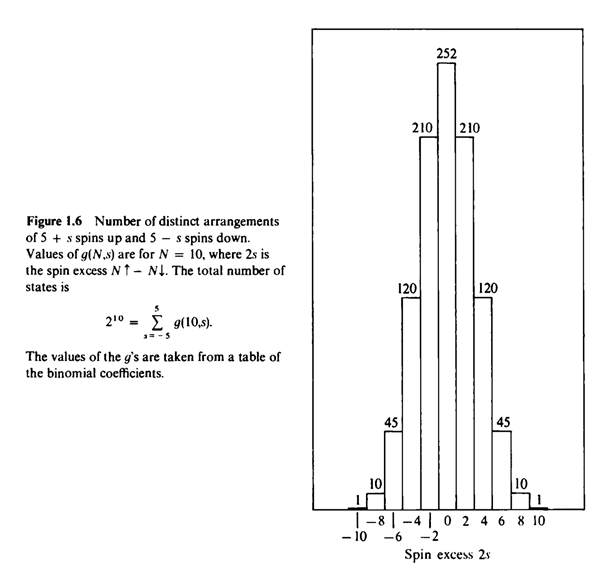
spin system 은 s= <s> 를 기점으로 대칭이다.
magnetic moment volume is
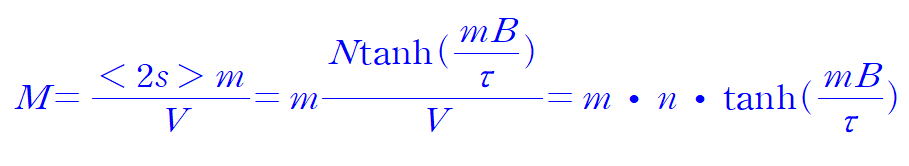
partition function for are one magnetic
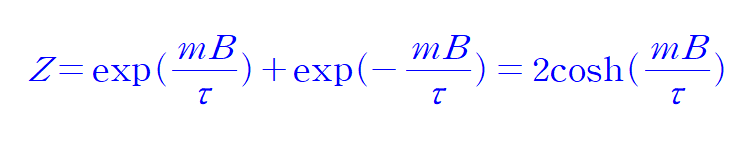
나중에 공부하게 될
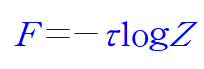
로 인해
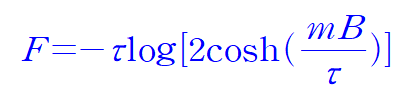
이때 N magnetic 일 때,
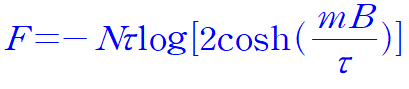
'열 물리학' 카테고리의 다른 글
| [열 물리학 23] IDEAL GAS(이상기체) and ideal gas law (이상기체 법칙) (0) | 2021.12.30 |
|---|---|
| [열 물리학 22] free energy 의 미분관계식 (0) | 2021.12.30 |
| [열 물리학 20] Thermodynamic Identity (열역학 항등식) (0) | 2021.12.30 |
| [열 물리학 19] reversible process (가역과정) 그리고 Pressure (압력) (0) | 2021.12.30 |
| [열 물리학 18] Boltzman distribution function (볼츠만 분포함수) (0) | 2021.12.27 |