2021. 12. 30. 04:43ㆍ열 물리학
가끔 포스팅 할때 영어로 작성하는 이유는 저로인해 잘못된 지식을 습득하는 것을 최소화하기 위해서 입니다.
읽기 어려운 부분은 약간의 해석을 남기도록 노력하겠습니다.
앞에서 배운 Z, F를 모두 이용해보자!!
now consider one atom in a box of cube:$V=L^3$
From

로 인해 양자역학에서 particle in a box에서 공부했던 solution 은 다음과 같다.

where $n_x ,n_y , n_z $ are positive integer
오랜만에 봐서 기억이 안나겠지만 s는 state 이라는 것을 잊지말자 n 역시 state를 나타내는 quantum number 이다.

만약 증분이 매우 작다면, 즉 에너지가 높아지면서 간격이 매우 작아진다면

우리는 급수를 적분으로 근사할 수 있다.



n=1/V 이유는 N=1 이기 때문이다.
what is quantum concentration (양자 밀도) =one atom / cube of de Bro wavelength $\lambda $
de bro length를 roughly하게 계산해보면

(대략적인 계산을 한 이유를 보면 열 평형 속도가 다양하게 정의되고 있기 때문이다. 다음 페이지를 참고해보라 https://en.wikipedia.org/wiki/Thermal_velocity )
양자밀도는 다음과 같이 나타난다.
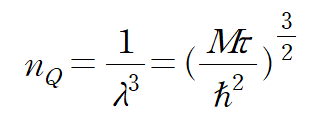
ex) For Helium concentration is

quantum concentration is

결과적으로


An ideal gas is defined as a gas of noninteracting atoms in the classical regime.
-> 클래식 영역이라면 이상기체로 볼 수 있다!
now The thermal average energy of the atom in the box : u

이전에 이런걸 배웠었다..


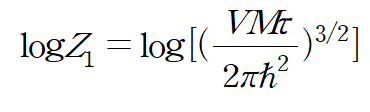

즉

$k_B$ is Boltzmann constant
The thermal average occupancy of a free particle orbital satisfies the inequality (자유 입자 궤도의 열 평균 점유율은 다음을 만족한다.)

-----------------------------------------------------------------------------------------------------------------------------------
[Example: N atoms in a box]
통계물리인데 N=1 이면 아쉽다고 생각할 것이다.
그래서 준비한 예제 N particle in a box! 이 예제는 6챕터인 이상기체 파트에서
다시 볼 식들이니 한번 공부해보자.
We first treat an ideal gas of N atoms in a box, all atoms of different species or different isotopes(동위원소)

(1) If we have one atom in each of N distinct boxes, the partition function is the product of the separate one atom partition functions:


분배함수가 곱셈으로 나타내는 이유: every independent state of the N boxes 그러한 상태의 에너지는

$\alpha , \beta .... , \zeta $ orbital indices of atoms in the successive boxes
그렇다면 위 결과는 N개의 박스에 입자들이 한 개씩 있다는 말이다.
이 말을 조금 틀어서 생각해보면 상호작용을 안하는 N개의 입자가 한 박스에 있어도 문제가 없다.(independent state 이므로)
(2) the partition function of N non-interacting atom of differencies in a single box


$\alpha , \beta .... , \zeta $ orbital indices of atoms in the successive boxes
같은 박스 안에 입자의 성질이 달라 봤자 입자의 질량 정도가 달랐을 것이다.
입자의 질량을 모두 갖게 하면

같은 입자가 N개 있다고 봐도 되겠다. but it overcounts the distinct states of the N identical particle system.
Particles of a single species are not distinguishable: 전자는 번호를 달지 않는다!
예시)
(1) 구분되는 입자가 두 개가 있을 때 partition function 은

그때 에너지는 분배함수 두 가지 상태 모두를 포함해야 한다.

(2) 동일한 입자가 두 개가 있을 때

이다. 하지만 이 둘은 구분이 불가능하므로 상태가 같다고 본다. 상태가 같으므로 분배함수의 상태 합에 단 한번만 포함해야 한다.
즉 $Z^N_1$ 은 상태를 $N!$ 만큼 나눠줘야 동일한 상태를 여러번 포함없이 분배함수를 쓸 수 있다.
고전영역(non interacting )에서의 1개의 상자 속 동일한 N개 입자의 분배함수는

(note) all occupied orbitals are always different orbital => valied assumption for $ n << n_Q $
이후 1/N! 인수에 대한 타당성은 다시 공부하게 될 것이다. 엔트로피는 실험적으로 측정가능하고 인수 N! 는 low concentration limit에서 정확하다고 한다.
----------------------------------------------------------------------------------------------------------------------------------
# 이상기체의 Energy
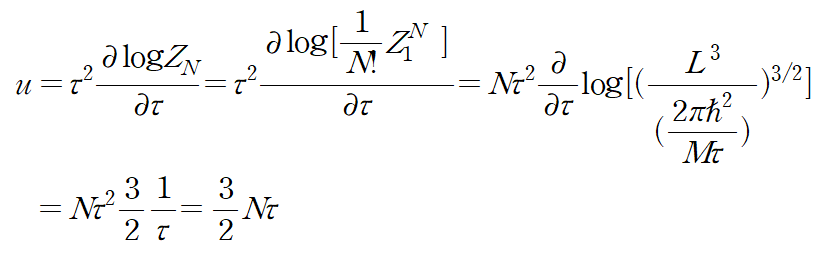
단일입자(N=1) 식과 일치함을 알 수 있다.
# 이상기체의 Free energy

이때 stirling 근사 식

이것을 위 식에 대입하면

이상기체의 free energy를 알게 되었다.
자유에너지를 알게 되면 분배함수도 알고 에너지도 알고 압력도 알 수 있다.
# 이상기체의 pressure
압력은

임을 알고 있다.

이므로
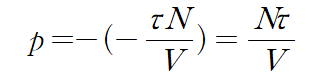
즉

를 얻어내고 이것을 이상기체 법칙 (ideal gas law) 이라고 한다.
#이상기체의 엔트로피

이다. 이상기체 엔트로피는 다음과 같다.

위 식은 Sackur –Tetrode 방정식으로 불린다.
추가로 다른 방법으로도 이상기체 에너지를 구할 수 있다. 엔트로피와 자유에너지를 알면

앞에서 얻어낸 에너지 식과 동일하다.
'열 물리학' 카테고리의 다른 글
| [열 물리학 25 ] Entropy of mixing (0) | 2021.12.30 |
|---|---|
| [열 물리학 24] Equilpartition of energy (에너지의 등분배) (0) | 2021.12.30 |
| [열 물리학 22] free energy 의 미분관계식 (0) | 2021.12.30 |
| [열 물리학 21] Helmholtz free energy (헬름홀츠 자유에너지) (0) | 2021.12.30 |
| [열 물리학 20] Thermodynamic Identity (열역학 항등식) (0) | 2021.12.30 |