[열 물리학 31] Thermal radiation and planck distribution (플랑크 분포 함수)

드디어 새로운 챕터입니다. 앞서 세가지 열 전달 방법중 복사에서 고전물리학으로 설명할 수 없게 되면서 문제를 해결하는 방법을 알아보았습니다. 이번 시간부터는 본격적으로 양자역학으로 열을 설명하는 첫번째 방법을 배우는 시간이라고 생각하면 되겠습니다.

 

planck Distribution function(플랑크 분포 함수)

플랑크 분포함수는 다음 세가지 결과를 만듭니다.

 

 

(1) planck Distribution function Describes the spectrum of thermal electromagnetic radiation in thermal equilibrium a cavity(열평형 공동)

->근사적으로 태양 또는 용접기로 가열된 금속에서 방출되는 스펙트럼도 설명하여 준다.

 

 

(2) First Application of quantum thermal Physics

 

 

(3) Thermal energy spectrum of lattice vibration of an electric solid

* mode a particular oscillation amplitude pattern in the cavity or in the solid $\omega = 2 \pi f$

 

 

 

 

characteristic feature:

a mode of oscillation frequency $\omega$ can be excited only in unit of guantum of energy: $\hbar \omega$ 

 

 

 

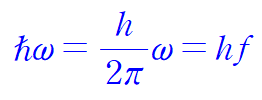
the energy $\epsilon_s$ of the state with “s” quanta in the mode :

(s=0,1,2,....positive integer)

 

여기서 s=0 일 때,

 

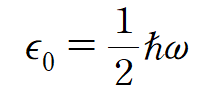
를 zero point energy 라고 양자역학에서 알려져 있다.

 

 

물리적으로는 zero point energy 가 의미가 있으나 수학적으로는 구조상 같으므로 생략하여 푼다.

 

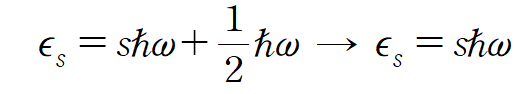
로 표현하자.

 

 

 

(참고) Differences between harmonic oscillator and $\epsilon_s =s \hbar \omega $ of the electromagnetic energy

 

#1 (harmonic oscillator) = (localized oscillator 국소적인 진동)

 

 

 

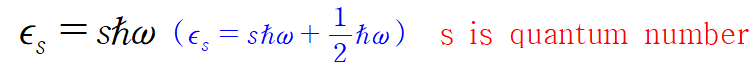
#2 electromagnetic energy is distributed within cavity ( mode)

 

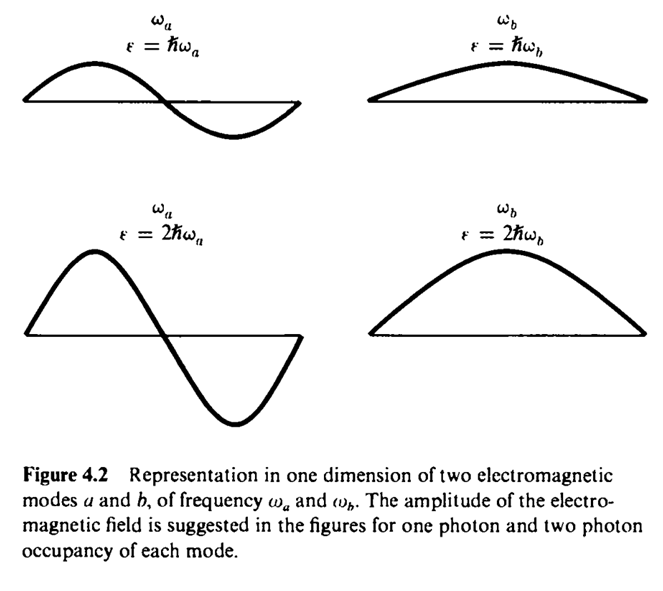
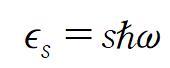
여기서는 s is number of photons in the mode

 

 

electromagnetic mode와 harmonic system 이 둘은 형태가 비슷해서 그렇지 사실은 다른 에너지이다. 조화진동은 zero point energy까지 생각해줘야 한다는 차이점이 있다. (electromagnetic mode는 cavity 전역에 존재하고 조화진동자는 입자 하나에 대한 설명이라는 차이점이다.)

(+ mode 라는 것은 어떠한 상황을 나타날 때 각기 다른 경우의 상태들을 말한다. (ex) 공이 구르는 mode 공이 튕기는 mode 등등등... 전자기파mode는 에너지가 커지면 빨리 진동하게 되니깐 $\omega$에 따라서 에너지가 달라질 것이다.)

 

 

 

 

# Thermal average of the number of photons in a mode when these phtons are in equilibrium with $\omega$ reservoir at $\tau$

 

열평형에서 phtons 의 분배함수를 살펴보자 (빛은 전자기파이며 photons 이며 열전도방법 중 복사 역시 전자기파의 전달이라는 점을 잊지말자.)

 

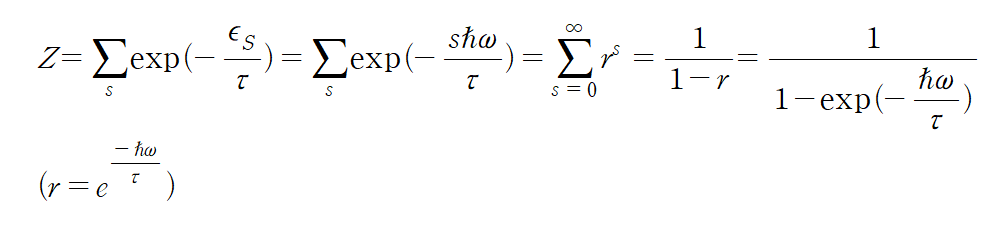
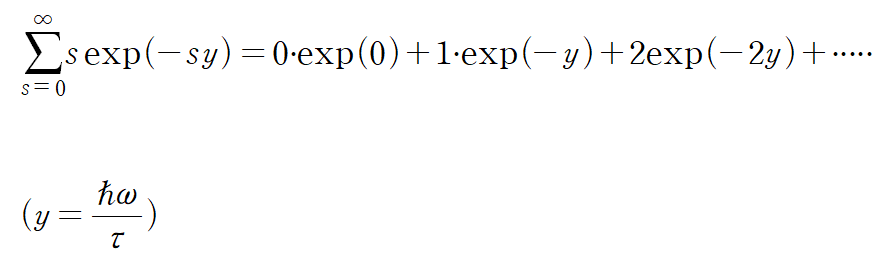
이라고 표현할 수 있겠지만.... convergence series 이라는 내용을 급수이론에서 알려져있습니다. (공부해봐요 재밌습니다....!) 그때 가지는 성질이 있는데...

 

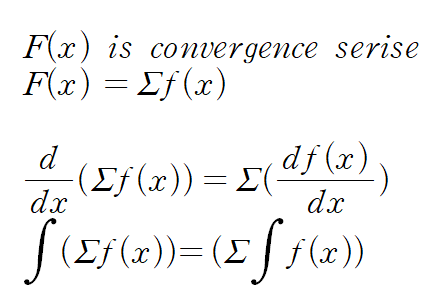
이게 성립됩니다!

사실 이걸 몰라도 자연은 수렴해야하니깐 ~ 물리학자 마인드로 수학은 넘어간다면

 

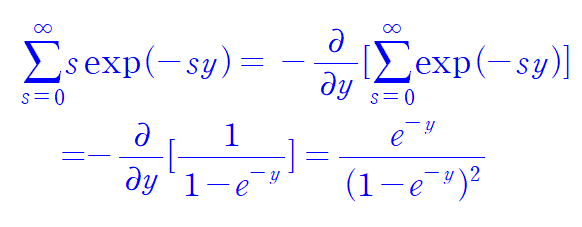
컴퓨터로 어려운 계산 수학으로 해결완료!

 

다시 본론으로 돌아가면

 

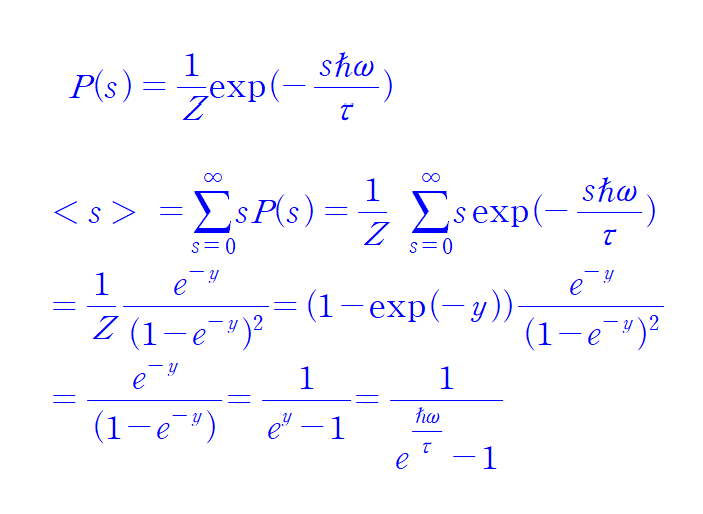
어라??? 어디서 많이봤는데.... 바로 전 포스팅에서 플랑크의 방식으로 구했던 식이 나왔습니다.

 

[Planck Distribution function for thermal average number of Photons in the mode $\omega$]

 

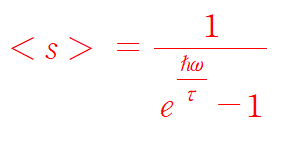
[The thermal average energy in the model]

 

 

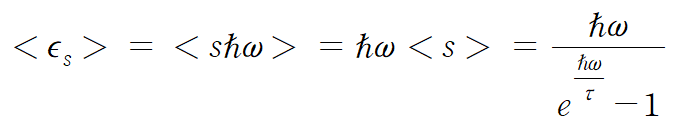
어라??? 어디서 많이봤는데.... 바로 전 포스팅에서 플랑크의 방식으로 구했던 식을 양자역학의 관점으로 풀어내었습니다. (https://zjvlvkdl.tistory.com/48)

 

(참고) In the classical limit $\tau >> \hbar \omega$

 

 

 

 

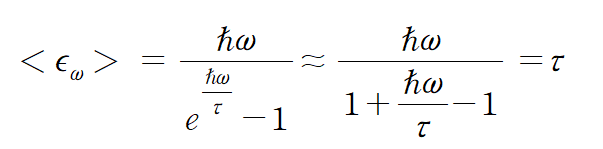
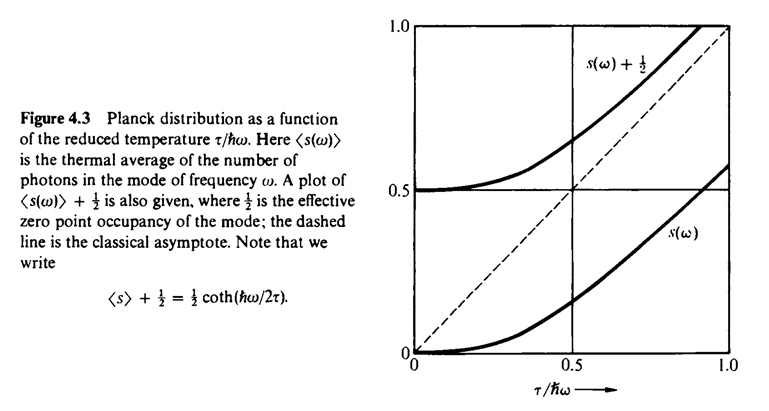
<s>함수 (또는 에너지함수 $<\epsilon >$)는 $\tau$가 높을수록 선형적으로 변함을 볼 수 있다.