2021. 12. 14. 20:19ㆍ열 물리학
많은 사람들이 봐주고 의견을 남겨주면 좋겠다.
이전부터 작성해둔 수식을 블로그 글에 옮기는 과정에서 화질이 깨질수 있다.
수식 작성에 관한 좋은 방법이 있다면 그역시 덧글로 남겨주길 바란다.
게시물 내용은 순서대로 읽는 것을 추천한다. 하지만 최대한 한 게시물 안에서 해결 할 수있도록 작성하겠다.
우선 열물리학을 공부하면서 기본적인 수학적인 이론부터 남기고자한다.
앞으로 많이 쓰이는 부분이기 때문에 이정도로 알아가면 좋을 것 같다.
<GAUSS INTEGRAL>

가우스 적분은 조금만 생각해보면 어렵지 않게 유도가 가능하다.
위 그림을 참고하면 미소 면적 dA 는 아주 작은 티끌세상이다. 직사각형 dA=dxdy 와 부채꼴의 일부에서 나온 면적 dA=dr(rdθ)는 무한히 작기 때문에 같다.
가우스 적분은 다음과 같다.
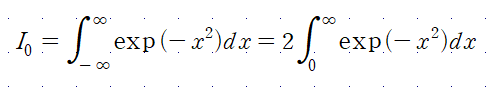
적분요소가 우함수이므로 미적분 기본정리에 의해서 대칭이다.

적분을 제곱을 하면 다음과 같다. x 와 y는 적분 후에는 무관하므로 둘다 x라 써두어도 상관은 없다.

로 치환하면

라는 결론이 나온다.
가우스 적분을 확장하자

여기서 감마함수를 정의 하겠다. (이 정의는 Mathematical Methods for Physicists 7/E 을 참고해보는 것도 좋은 공부가 될 것이다.)
m=0 인 상황을 보면....

가우스 적분의

값과 감마함수

의 값은 같음을 보였다.

또한

임을 알게 되었다.
m= 2 m=3 m=4 .... 전개를 해보면

다음과 같이 전개된다. (결과값은 감마 함수의 성질이다.)
이것을 일반화 하면

라는 결론이 나온다!!
'열 물리학' 카테고리의 다른 글
| [열 물리학 06] Sharpness of the Multiplicity Function (0) | 2021.12.15 |
|---|---|
| [열 물리학 05]Binary Alloy(합금) system (0) | 2021.12.15 |
| [열 물리학 04] Multiplicity function (0) | 2021.12.15 |
| [열 물리학 03] states of a model system (0) | 2021.12.15 |
| [열 물리학 02] Stirling Approximation 스털링 근사 (0) | 2021.12.14 |