[열 물리학 02] Stirling Approximation 스털링 근사
2021. 12. 14. 20:54ㆍ열 물리학
728x90
stirling approximation 역시 열 물리학에서의 큰수의 계산을 도와주는 수학적지식이다.
앞 게시물과 이어지며 한번씩 정독해보길 바란다.
아래 식이 우리가 말하는 스털링 근사이다.

n이 클 때 위과 같이 근사가 가능하다.
위 식을 구하는게 이번 포스팅의 목표이다.

저번 게시물의 결과인 위 식을 그대로 가져와서 쓰겠다.

x를 위와 같이 치환해보자. 그러면...

이 된다. f(x) 가 되는 이유는 아래식으로 증명할 수있습니다.

f(x)를 대입하면

이때
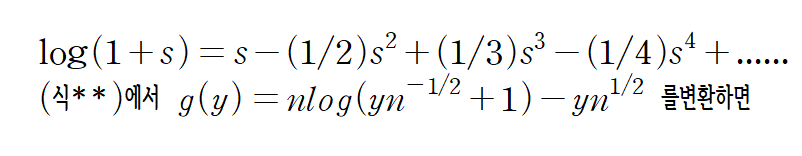

이 된다.

의 첫 번째 항의 로그만 보면


즉 g(y) 는

다시 처음으로 돌아가면 다음처럼 바뀌겠다.우리는 n이 아주 큰 상황이다 하한선을 마이너스 무한으로 보내면 다음과 같다.


적분 일부는 이런데~~ exp(O(s^3)) 은 어떻게 처리할까..???
이 다음부터는 책에서도 지루한작업(tedious work) 이라고 한다.
그래도 남은 term이 왜 나오는지 정도는 보는 차원으로 확인만 해보자.
우리는 물리학이니깐 수학자처럼 증명은 안하더라도 매칭은 시킬 수 있으니 그렇게라도 증명하자.
A를 찾아서 1/(12n) term 을 만들어보자

라고 정의한 후 서로 빼보면....
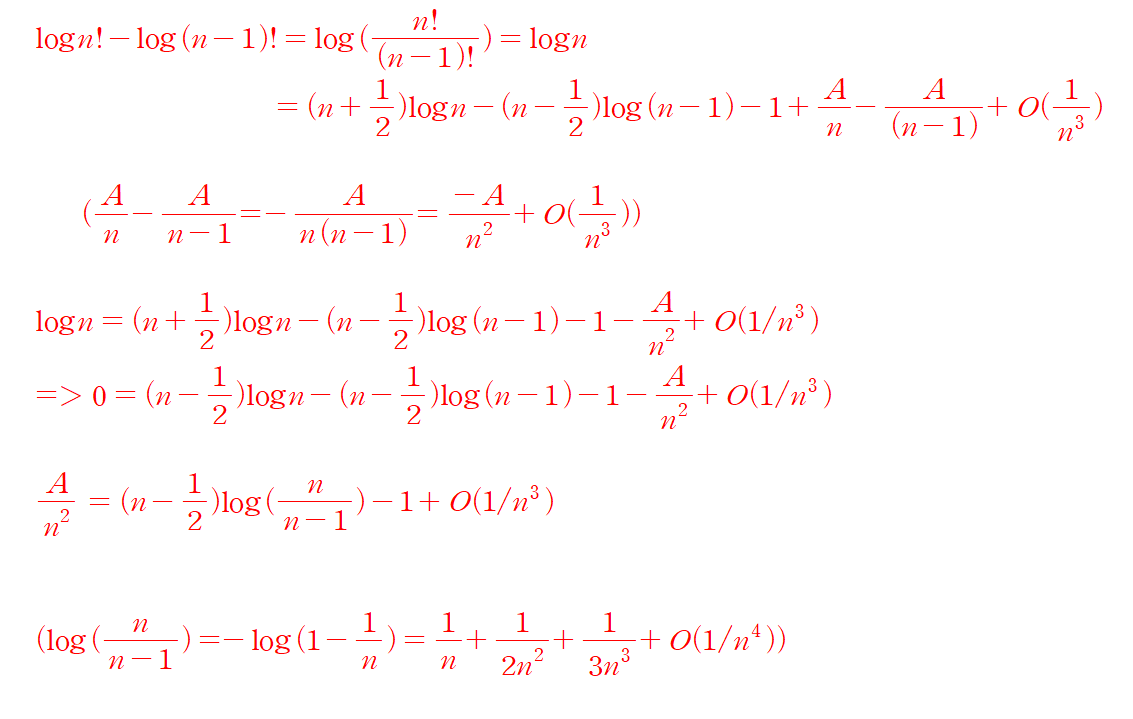
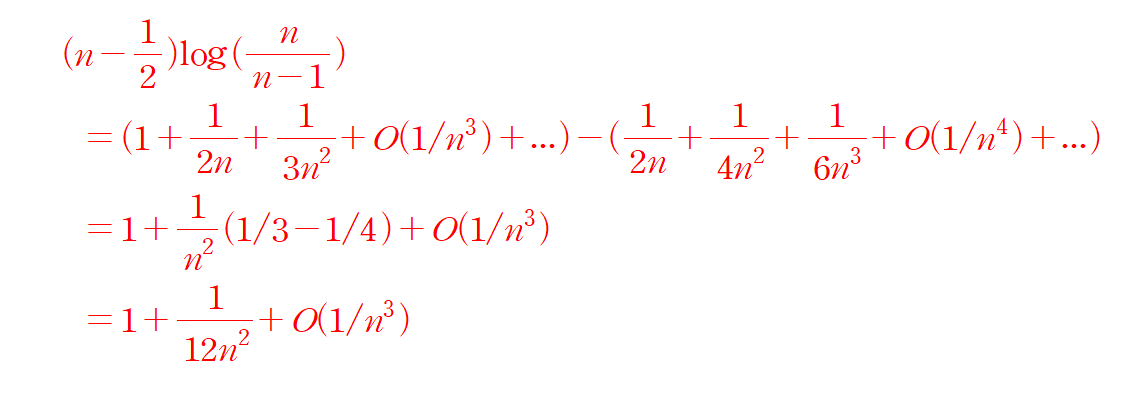
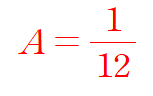
A 값이 1/12 임을 알았으니....


라는 결론이 나온다.(1장에서 쓰일꺼임~~)
증명완료.
때때론 간소하게

를 쓰기도 한다.
728x90
'열 물리학' 카테고리의 다른 글
| [열 물리학 06] Sharpness of the Multiplicity Function (0) | 2021.12.15 |
|---|---|
| [열 물리학 05]Binary Alloy(합금) system (0) | 2021.12.15 |
| [열 물리학 04] Multiplicity function (0) | 2021.12.15 |
| [열 물리학 03] states of a model system (0) | 2021.12.15 |
| [열 물리학 01] GAUSS INTEGRAL and gamma function (가우스적분 과 감마함수) (0) | 2021.12.14 |